前言
在这篇文章中,我们将会一起学习二分算法,比上一章的滑动窗口要难上许多(对我来说)。
话不多说,我们直接开始。
1.二分算法的基本定义
一句话概括本质:通过判断左右边界所围成区域的中点的值和目标值的关系,来决定下一步要在该区域的哪半边继续进行同样的操作,直到触发循环的退出条件。
讲一讲流程就是(以左右闭区间为例):假设我们拿到一个升序的序列nums和要查找的目标值target,那么我们开局将左边界left和右边界right都设立在这个序列的两头(举个例子,0和len(nums)-1),进入循环后先取它的中点mid,判断nums[mid]的值:
如果nums[mid]≥target,那就选择左半边进行下一步,使right=mid-1;反之,选择右半边进行下一步,使left=mid+1。
周而复始,直到触发循环的退出条件(此处是left>right退出)。
2.如何进一步理解二分算法-红蓝染色法
可以先去看这个视频:【算法入门】用红蓝染色法学爆二分查找
在红蓝染色法中,我们将一个升序数组分成蓝区(<目标值的区域),空白区和红区(>=目标值的区域)。我们二分就是把对应的元素染色到对应的区域。
在这个视频中,博主介绍了三种二分类型,分别是左右开区间、左右闭区间以及左闭右开区间。为了方便,本文章统一使用左右闭区间,即[l,r]。
在这个视频中,左右闭区间类型的二分算法在循环结束后,有一件事情是永远不变的,无论红蓝区的标准如何调整:l在红区的最左边,r在蓝区的最右边。如下图所示:
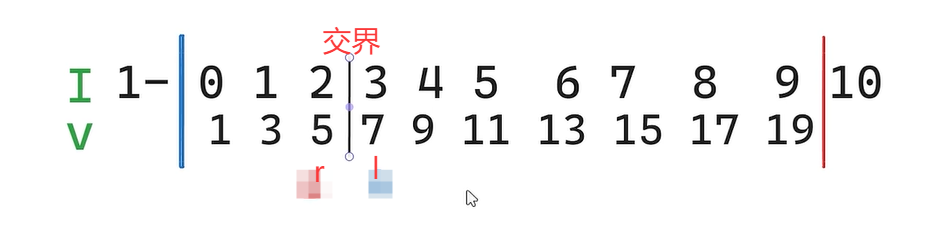
并且,按照我上面的分区设定,l会正好指在target上面(如果有),如果没有target,会指在大于它的第一个数上面。所以如果你要找target或者大于它的第一个数,直接输出nums[l]就行了。
那么遇到其他类型又怎么办呢?假设题目就是想让我找>target的第一个数,并且nums中有可能本身就有target,如果还是按照上面的标准划定红蓝区,那么就有可能直接输出target了,这咋整呢?
先记住上面永远不变的事情,然后我们再去调整蓝区和红区的标准,就能做到这件事:把红区调整成>target的数全都在这里面,把蓝区调整成≤target的数全都在这里面。再看看上面永远不变的事情,是不是l自然而然就指到了比target大的第一个数上,并且即使有target,也不会指到target上。
那么反映到代码上,又会变成咋样呢?
先看看最上面情况的代码(蓝区是<目标值的区域,红区是>=目标值的区域):
int lower_bound(vector<int>& nums,int target){
int l=0,r=nums.size()-1;
while (l<=r){
int mid=(l+r)/2;
//下面这一行代码是最关键的,是决定红蓝区域性质的核心代码
if (nums[mid]<target){ //由于l左边(不包含它自己)是蓝区,如果nums[mid]<target,
l=mid+1; //那么将其收入蓝区;
}else{ //如果nums[mid]≥target,
r=mid-1; //将其收入红区
}
}
return l;//输出红区的最左边的元素
}结合注释看,你现在一定有所体会了吧?所以,如果我们要求大于target的第一个数,那就按照上面的标准来更改红蓝区:把红区调整成>target的数全都在这里面,把蓝区调整成≤target的数全都在这里面。
int lower_bound(vector<int>& nums,int target){
int l=0,r=nums.size()-1;
while (l<=r){
int mid=(l+r)/2;
if (nums[mid]<=target){ //由于l左边(不包含它自己)是蓝区,如果nums[mid]<=target,
l=mid+1; //那么将其收入蓝区;
}else{ //如果nums[mid]>target,
r=mid-1; //将其收入红区
}
}
return l;//输出红区的最左边的元素
}这样一讲,是不是小于target的第一个数等等情况,你也能解决了?
如果要找小于target的第一个数,就直接将蓝区改成<target,红区改成≥target,最后l-1就是答案的位置(如果算出来是-1,说明不存在,target就是最小的数)。
其他情况就不讲了,举一反三即可。
3.题目实战——二分查找型 0809更新
做了4天的题目(当然也只限于白天的时间做,晚上或者接近晚上时我要三角洲启动),属于是要给我燃尽了。这个难度真的比滑动窗口难多了。滑动窗口是这样的:简单题直接秒,中等题有的能秒有的得稍微想想,hard题目有点难度,有的能想出来,没想出来的看题解后也能豁然开朗;二分呢?简单题我得想想到底哪里能用到二分,中等题我绞尽脑汁,hard题连题解也看不懂。

别问我为啥中间空着一些题目没做,大部分的题目都是涉及到类(class)等等的概念(除了3488和两道会员题之外其他都是),我连题意都难以理解,更别说做出来了。等其他正常的算法题做完之后,我再回过头来学习学习类的概念,在其他类型题目的章节中挑几题讲讲。
在做出来的题目之中,以下题目是我没使用二分算法做出来的,因为我没想到哪里能用到二分,所以也排除在此次讲解名单之外:
感兴趣的同学可以自己去做做看。排除掉上面这些题目,剩下的题目,我来挑一些讲解。除了简单题,中等及以上的都有一个共同特质:都是10^5的数据规模,必须要利用二分去卡nlogn的时间复杂度,否则就超时。
那我们先从简单题开始吧。
3.1 简单题:利用红蓝染色法掌控left指针最终落点
由于在第二个章节中,我已经将红蓝染色法讲的比较细致了,所以我在这里题目的讲解中会一笔带过。
先看第一题:34. 在排序数组中查找元素的第一个和最后一个位置
这道题要求我们找到升序数组中重复元素所在的区间。换句话说,我们只需要二分两次,第一次确定该元素最开始的点位,第二次确定比该元素大1的元素的位置。是时候请出红蓝染色法了!
设定红蓝规则如下:蓝区包含<target的数,红区包含>=target的数,由于left指针一定会落在红区的最左边第一位,所以left指向的要么是target,要么是比target大的第一个数。
所以在我们的第一次二分中,直接取left就是该元素的左区间。再加个判断:如果nums[left]≠target或者left超出了数组右边界1格,说明不存在该元素,我们直接返回[-1,-1],都不需要做第二次二分了。
如果第一次二分找到了,没退出,那就继续第二次二分。我们需要找到该元素的右边界。继续沿用上面的红蓝规则,我们直接代入target+1,这样最后left一定会停在target+1这个数或者比target+1大的第一个数上,那此时的left-1就一定是target。这时候就不需要判断了,left最多超出数组右边界1格,left-1是一定在界内的(建立在第一次二分合法的前提下)。
看代码:
class Solution {
public:
int lower_bound(vector<int>& nums, int target){
int l=0,r=nums.size()-1;
while (l<=r){
int mid = (l+r)/2;
if (nums[mid]<target){ //因为left左边是蓝区
l = mid+1; //所以按照职责的划分,小于target的数会被l扫过去,进入蓝区,包括nums[mid]本身
}else{ //二分代码的核心就在这几行,别的没啥好讲解的
r = mid-1;
}
}
return l;
}
vector<int> searchRange(vector<int>& nums, int target) { //解题主程序
int start = lower_bound(nums,target); //查找该元素左边界
if (start==nums.size() || nums[start]!=target){ //按照上面所说的,进行合法性判定
return vector<int>{-1,-1}; //若非法,说明没找到
}
int end = lower_bound(nums,target+1)-1; //按照上面所说的,找右边界
return vector<int>{start,end};
}
};剩下的基础题目中,下列题目都是和本题一样的红蓝规则,我就不重复讲解了:
但是有一道题是例外,它的红蓝规则和本题一样,但是我用到了一个新东西——保存答案并提前退出。
请看第二题:704. 二分查找
其实呢,这道题不用这个新东西也是能做的,就是稍微麻烦一点:在循环退出后,判断left指针是否越界、指向的是不是target,如果是就说明找到了,否则就是没找到。
但是,用了这个方法后,我们只需要起一个ans变量,令它初始等于找不到就要返回的值(本题是-1),并且在二分的判断中插入一条对nums[mid]是否等于target的判断语句,如果是,就将mid存入ans,然后直接break。事后不需要任何判断,直接就能返回ans。
class Solution {
public:
int search(vector<int>& nums, int target) {
int l=0,r=nums.size()-1,ans=-1;
while (l<=r){
int mid=(l+r)/2;
if (nums[mid]<target){ //一样的红蓝规则
l=mid+1;
}else if (nums[mid]==target){ //中途插入是否相等的判断
ans=mid;
break;
}else{
r=mid-1;
}
}
return ans;
}
};接着我们来讲第三题:744. 寻找比目标字母大的最小字母。这题的红蓝规则和前面两题不一样,让我们一步步来寻找新的规则。
它要找比目标字母大的第一个字母,也就是我就算找到了目标字母,也不行,得去找比它大的第一个字母。
这种情况下,我们直接令红蓝规则如下:蓝区包含<=target的字母,红区包含>target的字母。
由于left一定会落在红区最左边第一个,所以自然而然就落在了比目标字母大的第一个字母上。是不是非常巧?
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
int l=0,r=letters.size()-1;
while (l<=r){
int mid=(l+r)/2;
if (letters[mid]<=target){ //蓝区包含<=target的字母
l=mid+1;
}else{
r=mid-1;
}
}
if (l==letters.size()){ //如果left超出了数组右边界,说明没找到
return letters[0]; //按照题目要求返回第一个字母
}
return letters[l];
}
};至此,二分查找的基础题目已经过了一遍。如果上面3题全都掌握,那么你已经基本上掌握了红蓝染色法的精髓。
3.2 中等题以及hard题:nlogn是我的底线
这一部分的题目,我很难去归纳出几种类型。因为这和上一个滑动窗口的难题一样,重点不在二分查找本身,而是你不知道你该拿二分查找去干啥,在动用二分查找之前该如何转换题目的条件。
所以,如果强行归纳,那么这些题目有一个共同点:拿一连串的询问去一串数组里面二分查询啥东西,并且还把排序这个数组的工作交到了你手上,时间复杂度nlogn,别的没了。
所以,学会使用各个主流竞赛语言的内建排序方法还是非常重要的,下面来盘点一下。
3.2.1 各个主流竞赛语言的内建排序方法
1.c++的内建排序方法
int main(){
vector<int> nums = {1,1,4,5,1,4}; //初始化数组
sort(nums.begin(),nums.end());//升序排序
sort(nums.begin(),nums.end(),[](auto& a,auto& b){ //降序排序
return a>b; //此处使用lambda规则,其中a和b代指前一个元素和后一个元素,a>b即为我希望前一个比后一个大,实现降序排序
});
}2.c++使用lambda对二维数组进行自定义排序
当然这里可以灵活应变,换成pair也是可以的。cpp的lambda还是比较好理解的,我是直接死记硬背的,反正目前就这个场景会用到。
int main(){
vector<vector<int>> matrix = {{1,2,3},{5,4,6},{8,9,7}};
sort(nums.begin(),nums.end(),[](auto& a,auto& b){ //这里的a和b代指拨开matrix的第一层元素,即{1,2,3}这样的
return a[0]<b[0]; //这里的意思是取第一位进行比较,即按照第一位的大小进行降序排序
})
}3.python的内建排序方法(包含lambda自定义排序语句,若有不懂,请先去学习python的lambda语句)
nums = [1,1,4,5,1,4]
nums.sort() #升序排序,直接改变nums本身
nums.sort(reverse=True) #降序排序
sortedNums = sorted(nums) #升序排序,不直接改变nums本身,需要自己拷贝
sortedNums = sorted(nums,reverse=True) #降序排序,不直接改变nums本身,需要自己拷贝
matrix = [[1,2,3],[4,5,6],[7,8,9]]
matrix.sort(key=lambda x:x[0]) #此处是按照子列表的第一个数的大小进行升序排序
matrix.sort(key=lambda x:x[0],reverse=True) #此处是按照子列表的第一个数的大小进行降序排序4.Go的内建排序方法
不讲它的自定义排序了,纯纯路边,竞赛用这个纯属浪费时间。想学的去滑动窗口的文章里面找,那里面有。
sort.Ints([]int)
升序排序 int 切片。sort.Float64s([]float64)
升序排序 float64 切片。sort.Strings([]string)
升序排序 string 切片。
不多说。
3.2.2 正式开始题目实战
首先看第一题:1170. 比较字符串最小字母出现频次
我们需要分成两步来解决这个题目。首先解决这个f(s)函数,再利用这个函数去解决题目的问题。
如何写这个f(s)函数呢?在这道题目,由于用例比较水,所以你直接遍历数次数也是可以的。但是我们这次学的是二分算法,所以我们可以先排序,后二分:将字符串按照字母序升序排序后,利用二分找重复字母的左边界和右边界,然后减一减就是出现次数(和上面34. 在排序数组中查找元素的第一个和最后一个位置是一样的)。
int f(string s){
//1.给字符串排序 aaazz
sort(s.begin(),s.end());
//2.找最小字母
char target = s[0];
//3.二分找边界
int l = 0,r = s.size()-1;
while (l<=r){
int mid = (l+r)/2;
if (s[mid]<=target){ //<=的放蓝区
l = mid+1;
}else{
r = mid-1;
}
}
return l; //左边界最终落点即为出现次数
}接下来开始解决题目要求的问题。我们可以看到,题目中的比较都是f(s)求值后的数字之间的比较,所以我们需要先遍历queries和words,一个个调用f(s)将其转换成频率的数值并存入数组。接下来我们只需要对着两个数组处理问题即可。
接下来,我们需要获取需统计 words 中满足 f(queries[i]) < f(W) 的 词的数目,并且W 表示词汇表 words 中的每个词。这说明我们可以继续使用二分——一个个取出queries[i],事先将words数组排序好,然后用二分去找queries[i],设定蓝区为<=,红区为>,这样最后left一定指向大于 f(queries[i]) 的第一个数。最后再用数组长度-left,直接得出答案。
class Solution {
public:
int f(string s){}//此处省略,同上
vector<int> numSmallerByFrequency(vector<string>& queries, vector<string>& words) {
//1.把queries和words全部转换成数组
vector <int> qs,ws,ans;
for (int i=0;i<queries.size();i++){
qs.emplace_back(f(queries[i]));
}
for (int i=0;i<words.size();i++){
ws.emplace_back(f(words[i]));
}
//2.给ws排序
sort(ws.begin(),ws.end());
//3.单独拎出qs,一个个和ws对比
for (int i=0;i<qs.size();i++){
int k = qs[i],l = 0,r = ws.size()-1;
while (l<=r){
int mid = (l+r)/2;
if (ws[mid]<=k){
l = mid+1;
}else{
r = mid-1;
}
}
ans.emplace_back(ws.size()-l);
}
return ans;
}
};接下来来到难度上升的第二题:2563. 统计公平数对的数目
这道题,我们需要解决如何计算符合条件的对数。仔细看看题目条件:lower <= nums[i] + nums[j] <= upper,且0 <= i < j < n——按照以往的做题经验,我们只需要揪住其中一个不放,让另一个动起来就行了。否则两个都在动,我们不好处理。那么具体怎么操作呢?
看看数据规模,依旧是我们熟悉的10^5,这注定我们的时间复杂度不能超过nlogn,自然而然想到了第一层枚举+第二层二分。我们将nums[i]移项到两边,这样我们的不等式就变成了lower-nums[i] <= nums[j] <= upper-nums[i],这样我们不是只需要找到符合条件的nums[j]就行了?这样我们就形成了一个基本框架:将数组提前排序好,一层循环遍历找nums[i],二层二分找符合条件的nums[j]的左边界和右边界,这样我们就能在规定的时间复杂度内完成这道题目。
接下来来解决第二个问题:我们该设定咋样的红蓝规则来找到左右边界呢?为了方便,我们规定我们所寻找的是闭区间(像[1,3]这样的),在本题中,就是[lower-nums[i],upper-nums[i]]这样的区间。先找左边界的位置,我们令蓝区为<,红区为>=,这样left天然就会落在左边界上;再找右边界,我们令蓝区为<=,红区为>,这样left-1就一定会落在右边界的位置。由于上面对红蓝染色法铺垫了太多,此处我讲的十分简略。如果这里你看不懂,退回去从头开始看就行了(那个视频也要看)。
这样,我们就知道该如何寻找符合条件的数的左右边界了。接下来还有最后一个问题——计算组数,这也是个难点。由于组数和两个数字的顺序无关,所以为了防止重复,我们只关注第一层枚举出来的数的后面的数,这个数后面有几个符合条件的数,我们就将其与这个数连线,就构成了几个数对。由于我们二分查找的范围是整个数组,有时候left边界甚至left、right两个边界会一起跑到我们枚举的i的左边去,这时候就需要我们加以判断并做出处理,这是决定这道题目能不能做对的关键。
首先,如果left超出数组的边界咋整?这说明这个数组里面的数都太小了,没一个数是能符合lower-nums[i]的标准的,这种情况直接跳过,没一个能累加的。其次,如果right<=i呢?按照我们上面不重复的原则,这样也是不能累加的。那么,如果i被夹在left和right中间呢?此时,只需要取max(left,i+1)作为左边界就行了,我们需要主动舍弃<i+1的部分,因为这样会重复。
至此,本题思路讲述完毕,比上一题多了一些巧思,尤其在边界处理上还是有些难度,上代码:
class Solution {
public:
long long upper_bound(vector<int>& nums, int upper){ //找右边界
int l=0,r=nums.size()-1;
while (l<=r){
int mid = l+(r-l)/2;
if (nums[mid]<=upper){
l = mid+1;
}else{
r = mid-1;
}
}
return l-1;
}
long long lower_bound(vector<int>& nums, int lower){ //找左边界
int l=0,r=nums.size()-1;
while (l<=r){
int mid = l+(r-l)/2;
if (nums[mid]<lower){
l = mid+1;
}else{
r = mid-1;
}
}
return l;
}
long long countFairPairs(vector<int>& nums, int lower, int upper) {
//1.给nums排序
sort(nums.begin(),nums.end());
//2.开始二分找合格的数字的范围并累加
long long sum = 0;
for (int i=0;i<nums.size()-1;i++){
int k = nums[i],low = lower-k,up = upper-k; //这里是对原不等式的移项操作
int left = lower_bound(nums,low);
int right = upper_bound(nums,up);
if (left>=nums.size() || right<=i){ //很重要的判断
continue;
}
sum+=right-max(left,i+1)+1; //处理i夹在l和r中间的情况
}
return sum;
}
};接下来来到第三题:LCP 08. 剧情触发时间
这道题比第二题略微简单一些,和第一题难度差不多,这是我主观上的感受,因为我想了一会也算是想出来了。
主要思路就是这样:把每日的递增量累加起来,自然而然就形成了一个每个值都上升的二维数组;然后单独拎出每个剧情触发的要求requirements[i],里面有三个数,我们再单独拎出其中的每个数requirements[i][j],使用二分找到它开始达标的第一天的位置(红蓝规则如下:蓝区<,红区>=,这样left的落点就是刚刚开始达标的第一天的位置),把三个数的位置都找出来并记录,最后选出最大(最靠右)的那个位置,就是3个全都达标的天数。这利用了每个值都上升的特性,只要前面达标了,不管多后面它都会达标。
这题是真正的巧思,如果没想到这一点,用其他方法我也不知道怎么做。上代码:
class Solution {
public:
int betterMax(vector<int> nums){ //用来求数组最大值的函数
int maxNum=nums[0]; //所以cpp和go能不能学一下python的max()?尤其是go
for (auto x:nums){
maxNum=max(maxNum,x);
}
return maxNum;
}
vector<int> getTriggerTime(vector<vector<int>>& increase, vector<vector<int>>& requirements) {
//1.写出自动升序的实时属性数量
vector<vector<int>> curNum(increase.size()+1,vector<int>(3,0));
for (int i=1;i<=increase.size();i++){
for (int j=0;j<3;j++){
curNum[i][j]=increase[i-1][j]+curNum[i-1][j]; //累加增量,此事在前缀和中亦有记载
}
}
//2.遍历reqs
vector<int> ans(requirements.size(),-1);
for (int i=0;i<requirements.size();i++){
vector<int> tempAns(3,0);
bool flag = true; //触发器,如果其中有一个属性无法在规定天数内达到要求,就直接退出,没必要再算后面的属性了
for (int j=0;j<3;j++){
int req = requirements[i][j],l=0,r=curNum.size()-1;
while (l<=r){ //二分找开始的天数
int mid = l+(r-l)/2;
if (curNum[mid][j]<req){
l = mid+1;
}else{
r = mid-1;
}
}
if (l>curNum.size()-1){ //如果left落在了最后一位,说明
flag=false;
break;
}
tempAns[j]=l;
}
if (!flag){
continue;
}
ans[i]=betterMax(tempAns);
}
return ans;
}
};接下来来到第四题:2070. 每一个查询的最大美丽值,从这道题开始,还有下面的第五题,我都没想出来,看题解做出来的,好在题解也是看懂了。
看完题目了?那就先看题解吧:灵神的题解,看里面的方法二,方法一我没看懂。
方法二的精髓是这个《左侧最大值》的算法,这使得我们可以直接对着处理好的数组二分查找,十分方便。
看看我的代码:
class Solution {
public:
vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {
//1.按照价格大小排序
sort(items.begin(),items.end(),[](auto& a,auto& b){
return a[0]<b[0];
});
//2.原地构建左边的最大美丽值
for (int i=1;i<items.size();i++){
items[i][1]=max(items[i-1][1],items[i][1]);
}
//3.二分查找价格的正确位置
vector<int> ans(queries.size(),0);
for (int i=0;i<queries.size();i++){
int l=0,r=items.size()-1,k = queries[i];
while (l<=r){
int mid = l+(r-l)/2;
if (items[mid][0]<=k){
l = mid+1;
}else{
r = mid-1;
}
}
if (l-1>=0){ //这里依旧需要留心处理边界
ans[i]=items[l-1][1];
}
}
return ans;
}
};接下来来到本次讲解的最后一题,第五题:1818. 绝对差值和
看完题解后,我豁然开朗,但是仍然有一点搞不明白:它为何不处理重复取元素的情况?毕竟nums1和nums12,后者排序了,去后者二分查找是极有可能找到一个和前者nums1[i]相等的元素的。
后面明白了:即使重复了又如何?重复找到了最小的元素,不就说明我不需要用别的元素替换自己吗。毕竟题目也没强制要求必须替换。
贴上我的代码:
class Solution {
public:
int minAbsoluteSumDiff(vector<int>& nums1, vector<int>& nums2) {
//1.拷贝一份nums1,然后排序
vector<int> nums12=nums1;
sort(nums12.begin(),nums12.end());
//2.对于nums1中的每一个元素,二分找和nums2[i]最接近的元素,并一直累加
long long sum=0,mod=1000000007,maxDiff=-1;
for (int i=0;i<nums1.size();i++){
long long tempAns = abs(nums1[i]-nums2[i]),newAns=0;
sum+=tempAns;
int l=0,r=nums12.size()-1;
while (l<=r){
int mid = l+(r-l)/2;
if (nums12[mid]<nums2[i]){
l = mid+1;
}else{
r = mid-1;
}
}
if (l-1<0){ //
newAns = abs(nums12[l]-nums2[i]);
}else if (l>nums12.size()-1){
newAns = abs(nums12[l-1]-nums2[i]);
}else{
newAns = min(abs(nums12[l]-nums2[i]),abs(nums12[l-1]-nums2[i]));
}
if (abs(tempAns-newAns)>maxDiff){
maxDiff=abs(tempAns-newAns);
}
}
//3.直接sum-最大值就是答案
return (sum-maxDiff)%mod;
}
};至此,这一章节已经全部更新完毕。
4.题目实战——二分答案型
4.1 求最小 0814更新
4.1.1 简介
这一部分的题目,一句话概括:用二分算法去猜答案,然后再通过时间复杂度O(n)及以内的算法来判断我猜出来的答案对不对,再通过算法的计算结果来判断答案是大了还是小了,直到退出二分,即获得答案。
下面放一个偷来的代码模板,能很完美的概括这一系列的题目:
class Solution:
# 计算满足 check(x) == True 的最小整数 x
def binarySearchMin(self, nums: List[int]) -> int:
# 二分猜答案:判断 mid 是否满足题目要求
def check(mid: int) -> bool:
# TODO
left = # 循环不变量:check(left) 恒为 False
right = # 循环不变量:check(right) 恒为 True
while left + 1 < right: # 开区间不为空
mid = (left + right) // 2
if check(mid): # 说明 check(>= mid 的数) 均为 True
right = mid # 接下来在 (left, mid) 中二分答案
else: # 说明 check(<= mid 的数) 均为 False
left = mid # 接下来在 (mid, right) 中二分答案
# 循环结束后 left+1 = right
# 此时 check(left) == False 而 check(left+1) == check(right) == True
# 所以 right 就是最小的满足 check 的值
return right
这次的题目在前面也是偏简单的,主要是后面的一些题目真的挺难的。尤其是最后一题,我看题解也理解了半天。
其实二分算法本身是一样的,这种类型的题目,主要就两个难点:第一个,也是最主要的,就是判断答案是否正确的算法,这是区分各个题目的一个东西;第二个,就是对二分算法上下界的判断,也基本得预先处理题目中的数组才能给出明确的上下界。
我将上面的题目分为以下几类(是我自己做题的主观感受,如果想要客观评价,上方图片的顺序就是由简单到难):
1.基础题(我能较快做出来)
2.进阶题(我需要思考一下才能做出来)
3639. 变为活跃状态的最小时间 和 滑动窗口->不定长滑窗->求子数组个数->越长越合法 知识点梦幻联动(至少我的做法是这样) 讲解
1482. 制作 m 束花所需的最少天数 这应该是没有固定模板,手搓的检查算法
2594. 修车的最少时间 这题我也是受下面3296的启发才做出来的,如果没受启发,难度应该介于进阶和困难之间,比3296略简单
3.困难题(我想不出来,看了题解才能做出来)
3296. 移山所需的最少秒数 彻底干碎算法题目做太多的思维定式 讲解
475. 供暖器 又是一个新思路 讲解
4.地狱题(我看了题解还得理解很久,才能彻底弄懂)
其中会讲解的题目也已经在上面标记了出来。
4.1.2 部分题目的讲解
先讲解第一题:3639. 变为活跃状态的最小时间,先看题。
关键部分:
如果 子字符串 包含 至少 一个
'*',则认为该子字符串有效。如果字符串中 有效子字符串 的总数大于或等于
k,则称该字符串为 活跃 字符串。
看到这两句,你是不是想起了什么?没想起来的自己去https://blog.lecspace.com/index.php/archives/76/复习一下。
不卖关子了,这就是 滑动窗口->不定长滑窗->求子数组个数->越长越合法 这一部分的知识点。我们可以在第一层使用二分猜答案,再在第二层使用越小越合法的老知识点,对*进行计数,并数出满足上述条件的子数组个数,再把它和k比较,就完事。
看我的代码,有详细注释:
class Solution {
public:
int minTime(string s, vector<int>& order, int k) { //解题主程序
//1.找二分的上下界并初始化
long long l = 0,r = order.size()-1,ans=-1;
//2.开始二分
while (l<=r){
long long mid = l+(r-l)/2;
string newS = s; //复制一份字符串便于我们处理
for (int idx=0;idx<=mid;idx++){
newS[order[idx]]='*'; //按照题目要求替换字符串
}
//滑窗数符合要求的子字符串数量
long long left=0,cnt=0,count=0; //cnt是数*个数的,count是数符合条件的子数组个数的
for (long long right=0;right<newS.size();right++){
if (newS[right]=='*'){
cnt++;
}
while (cnt>=1){ //一直推到不符合条件为止
if (newS[left]=='*'){
cnt--;
}
left++;
}
count+=left;
}
//下面开始比较
if (count>=k){ //字符串中有效子字符串的总数大于或等于k
ans = mid; //事先记录下答案
r = mid-1; //去尝试更小的
}else{
l = mid+1;
}
}
return ans;
}
};接着来讲第二题:3296. 移山所需的最少秒数,先看题。
看完题目了,先看一下我当时看的题解。
这题属于是给我震惊到了。当时我看到题目的这个式子: workerTimes[i] + workerTimes[i] * 2 + ... + workerTimes[i] * x ,我第一时间想到的是去做一个前缀和,来处理1+2+3+...+x这个式子,然后后面就不知道该如何处理了。
首先,这个式子是一个很经典的等差数列,根本用不着前缀和,只需要用最经典的x(1+x)/2的等差数列求和公式就行了。
并且,我们二分的是答案——秒数。这个式子是算秒数的,如果你用前缀和,意味着你永远无法拆开这个式子,没法进行如题解一样的左右移项的操作,最终来达到化秒数这个结果成为能代入计算是否符合的变量。
知道要拆开式子后,这道题目最后的难点就是处理上下限了。题解讲的很清楚了,此处不再赘述。
class Solution {
public:
long long minNumberOfSeconds(int mountainHeight, vector<int>& workerTimes) {
//1.先找上下界
long long maxTime=workerTimes[0];
for (auto x:workerTimes){ //这里枚举workerTimes是为了找到最大的时间,用于计算上界
if (x>maxTime){
maxTime=x;
}
}
//2.开始二分答案
long long l=1,r=maxTime*mountainHeight*(mountainHeight+1)/2,minTime=r; //此处的r就是和题解一样计算上界
while (l<=r){
long long mid = l+(r-l)/2,total=0;
for (auto x:workerTimes){
long long k=mid/x,sqr = floor(sqrt(8*k+1)); //按照题解的思路进行开方计算
sqr = (long long)floor(sqrt(8.0L*k + 1.0L)); //此处要注意上下取整的处理
total += (sqr - 1) / 2; //由于结果越大越好,为了确保合法性,我们选择下取整
if (total >= mountainHeight) break; // 剪枝
}
if (total>=mountainHeight){ //经典的二分判断+结果记录
minTime=min(minTime,mid);
r = mid-1;
}else{
l = mid+1;
}
}
return minTime;
}
};看来做算法题,有时候也不能局限于算法技巧,数学上的一些知识也是可以运用的。
然后,来看看第三题:475. 供暖器,先看题。
看完题目来看题解。
这道题的题意还是比较好理解的,二分的目的性也很强,最主要的难点就是想出一个时间复杂度在O(n)之类的算法来验证我此次二分出来的半径是否合法。但是我怎么就是想不出来。
题解的思路也是非常新奇:直接摆脱传统二分模板,外层遍历每一个屋子,然后使用二分找离每个屋子最近的供暖器,然后每个屋子都遍历过去,维护一个距离的最大值,就是我们所求的最小半径。
看代码:
class Solution {
public:
int findRadius(vector<int>& houses, vector<int>& heaters) {
//1.升序排heaters
sort(heaters.begin(),heaters.end());
//2.遍历房屋,二分找离每个屋子最近的供暖器
int maxRange=0;
for (int i=0;i<houses.size();i++){
int target = houses[i],l=0,r=heaters.size()-1;
while (l<=r){ //二分找的是供暖器,不是答案
int mid = l+(r-l)/2;
if (heaters[mid]<target){
l = mid+1;
}else{
r = mid-1;
}
}
if (l==0){ //这里处理left停在数组第一个位置的情况
maxRange = max(maxRange,abs(heaters[l]-houses[i]));
}else if (r==heaters.size()-1){//这里处理right停在数组最后一个位置的情况
maxRange = max(maxRange,abs(heaters[r]-houses[i]));
}else{ //如果l和r都合法,那就取其中最小值,代表离的最近的取暖器,然后全局再维护一个最大值
maxRange = max(maxRange,min(abs(heaters[l]-houses[i]),abs(heaters[r]-houses[i])));
}
}
return maxRange;
}
};最后,我们来看第四题:3048. 标记所有下标的最早秒数 I,先看题。
看完题目了吗?是不是感觉题意很晦涩难懂?那么先不急着看题解,看看我偷来的别人对题目很形象的改写:
你有
n门课程需要考试,第 i 门课程需要用nums[i]天复习。同一天只能复习一门课程。在第
i天,你可以选择参加第changeIndices[i]门课程的考试。考试这一天不能复习。搞定所有课程的复习+考试,至少要多少天?
带着这个改写,再去想想。如果还是想不出来,那就看看题解吧。
这道题,虽说从框架上来看是经典的二分答案,但是判断这个天数够不够的过程还是非常反常规和难的。我对着这个题解写我自己的代码都费了好大一阵功夫。
class Solution {
public:
bool check(vector<int>& nums, vector<int>& changeIndices,int maxDay){
//找出每个下标的最后位置
vector<int> last(nums.size(),0);
for (int i=0;i<maxDay;i++){
last[changeIndices[i]-1]=max(last[changeIndices[i]-1],i+1);
}
//找出最靠后的下标位置,用于初步判断天数合法性
int maxPos=last[0];
for (auto x:last){
maxPos=max(maxPos,x);
if (x==0){
return false;
}
}
if (maxDay<maxPos) return false; //初步判断题目所给数组合法性
int cnt=0;
for (int t=1;t<=maxDay;t++){
if (last[changeIndices[t-1]-1]!=t){ //如果不是考试日
cnt++;
}else{ //如果是考试日
if (cnt<nums[changeIndices[t-1]-1]){
return false;
}
cnt-=nums[changeIndices[t-1]-1];
}
}
return true;
}
int earliestSecondToMarkIndices(vector<int>& nums, vector<int>& changeIndices) {
if (nums.size()>changeIndices.size()) return -1;
//1.确定上下界
int l=1,r=changeIndices.size();
//2.开始二分
int ans=-1;
while (l<=r){
int mid = l+(r-l)/2;
if (check(nums,changeIndices,mid)){
ans = mid;
r = mid-1;
}else{
l = mid+1;
}
}
return ans;
}
};4.2 求最大 0828更新
4.2.1 简介
好久不见。也是14天没更新了,因为最近事情比较多,类似于同学聚餐,亲戚拜访之类的,并且人也不在状态上,加上这一批的题目比上批难了不知道多少,于是做题速度就极其慢。经过14天的磕磕绊绊,我也总算是把我目前知识能解决的题目给做出来了,下面给这些题目分分类。求最大的二分框架,我就不另外介绍了,套路基本一致,不清楚的直接去看上面的4.1.1,把ans=mid下面这行的r=mid-1换成l=mid+1,下面else分支的也相应换过来就行了。

我将上面的题目分为以下几类(是我自己做题的主观感受,如果想要客观评价,上方图片的顺序就是由简单到难):
1.基础题(我能较快做出来)
2226. 每个小孩最多能分到多少糖果 二分猜答案去直接遍历就行了,比较容易想到
2.进阶题(我需要思考一下才能做出来)
2576. 求出最多标记下标 这题我其实看提示了 需要想到匹配k个最小的数和k个最大的数之间的对应位置 不然做不出 此题会讲解
2982. 找出出现至少三次的最长特殊子字符串 II 联动滑动窗口知识
1898. 可移除字符的最大数目 需要手写一个逻辑去一个个匹配字母 以判断是不是子序列
1802. 有界数组中指定下标处的最大值 此题卡O(logn),强制你用等差数列求和公式去求和,找公式里面的首项、末项、项数三个参数非常麻烦,本来如果允许O(nlogn),直接使用循环求值,边界会比较好找
1642. 可以到达的最远建筑 基本逻辑不难:梯子留给最高的落差用,其他落差用砖块堆。但是要注意分类讨论细节
3.困难题(我想不出来,看了题解才能做出来)
275. H 指数 II 这题属于是看了题解能秒懂的类型:顺着题目的逻辑从小到大列举一下,就知道如何二分了 此题会讲解
2861. 最大合金数 当时做的时候定式思维了,没反应过来二分是需要顺着题目的思路去验证是否正确,而是一边二分一边在那里尝试直接求出数量。如果脑子转过来了这题其实属于进阶题里面最难的一题 此题会讲解
2071. 你可以安排的最多任务数目 这题是典型的贪心:用最强的k个工人去做最简单的k个任务,最好不嗑药就能做掉最简单的任务,实在不行要嗑药就做嗑药后能做的最难任务。贪心逻辑好理解,代码实际的实现略有难度 此题会讲解
4.地狱题(我看了题解还得理解很久,才能彻底弄懂)
2141. 同时运行 N 台电脑的最长时间 主要是得理解题解里面把电池电量当成连续的来用的思想 此题会讲解
5.78题(题解里面需要用到我目前没掌握的,且难以快速掌握的知识解决题目,所以看了题解也无法做出)
3007. 价值和小于等于 K 的最大数字 需要用到数位DP 后面学到了再来补
2258. 逃离火灾 需要用到双数组 并且我bfs只是初学 并不是很熟练 陆陆续续尝试了三四个小时没做出来
4.2.2 部分题目的讲解
第一题:2576. 求出最多标记下标,先看题。
先看是否符合二分要求:看到2 * nums[i] <= nums[j]这个式子,我们肯定想让左边的数字尽量小,右边的数字尽量大。这样配对后,剩下的数字会自然而然的越来越接近,也就是更难满足这个式子。所以配对的数量越多,越难达到这个条件,有单调性,可以二分。
接着用贪心的思想思考:为了匹配的成功率更高,我们尽量将i指向最小的数字,j指向最大的数字。但是这样会存在浪费:原本我的nums[i]可以和更小的nums[j]匹配,此时如果拿去和最大的nums[j]匹配,这样会使得小的nums[j]更难与其他数字匹配,导致得到的不是最好的结果。
那么我们该如何匹配呢?贪心的总思想是对的,左边数字要尽量小,右边数字要尽量大。我们只需解决这个浪费的问题就行:将最小的k个数和最大的k个数里面,内部相对排名相等的数进行匹配。换成代码语言,就是将nums[i]和nums[n−k+i]进行匹配。为啥这样行得通呢?举个反例,假设最小数和最大数全都可以相互匹配,但是如果我拿最小数里面第一小的数去和最大数里面第二小的数匹配,那么最小数里面第二小的数就不一定保证能和最大数里面第一小的数匹配上。从正面比较难解释,但是从反面还是可以解释一下的。基本原理就是避免了“大材小用,结果小材没法大用”所导致的匹配失败。
class Solution {
public:
int maxNumOfMarkedIndices(vector<int>& nums) {
//1.先排序
sort(nums.begin(),nums.end());
//2.二分找上下界
int l=0,r=nums.size()/2,ans=0;
while (l<=r){
int mid = l+(r-l)/2;
bool flag=true;
for (int i=0;i<mid;i++){
if (nums[i]*2>nums[nums.size()-mid+i]){ //内部相对排名相等的数进行匹配
flag=false;
break;
}
}
if (flag){
ans = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return ans*2;
}
};接着进入困难区域。讲一下第二题:275. H 指数 II,先看题。
在我的个人理解上,判断一个题目能否二分的标准,除了答案是否和某个变量存在单调性之外,还有就是:题目是否方便直接求出答案。这道题目的定义,至少 有 h 篇论文分别被引用了至少 h 次,是非常抽象的一个定义,我几乎想不到能如何直接求出一个答案。但是,我去验证我猜的答案对不对却十分简单:先讲论文引用次数升序排序,假设我猜h=x,那我只需要验证后x篇论文的第一篇的引用次数是否大于等于x就行了。毕竟引用次数是上升的,如果最大的x篇论文的第一篇的引用次数都>=x,那么后面的一定全都符合,这就说明x是合法的。
言归正传,我们来正面推理一下为啥能用二分。先列举一下:如果我至少有4篇论文被引用的次数>=4次,那么我也至少有3篇论文被引用的次数>=3次,也至少有2篇论文被引用的次数>=2次,也至少有1篇论文被引用的次数>=1次,但是却不一定至少有5篇论文被引用的次数>=5次,属于是越小越容易合法的类型,具有单调性,可以二分。
知道这一点后,二分写起来就不难了,甚至不需要写什么遍历的逻辑,一个判断即可。
class Solution {
public:
int hIndex(vector<int>& citations) {
int l=1,r=citations.size(),ans=0;
while (l<=r){
int mid = l+(r-l)/2;
if (citations[citations.size()-mid]>=mid){ //验证后`x`篇论文的第一篇的引用次数是否大于等于`x`
ans = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return ans;
}
};接着来看第三题:2861. 最大合金数,先看题。
看完题后,若有不会,看题解。
这题和上一题我判断是否可以二分的“野方法”有异曲同工之妙:如果我要算出最多能制造的金属数量,我得考虑一大堆情况(我没看题解的时候就莫名其妙的朝这个方向去写了),但是如果我猜个答案再去验证其对错,我只需要考虑要用哪台机器做就行了,我此时的花费就可以很简单的正向计算出来,最后看看有没有超出预算就行了。至于到底用哪台机器做,只需要遍历一下就行了,如果全都做不出来就是做不出来,如果有一台能做出来就直接退出,说明这个数量是可行的。
至于单调性,这根本不需要推理,肯定是造的合金越多我的消耗越多,所以是一定有单调性的。
class Solution {
public:
int maxNumberOfAlloys(int n, int k, int budget, vector<vector<int>>& composition, vector<int>& stock, vector<int>& cost) {
//1.寻找上下界
long long l=0,minStock=stock[0];
for (auto x:stock) minStock = min(minStock,(long long)x);
long long r = budget+minStock,ans=0; // 这里的假设价格为1求上界我是真没想到,太妙了
//2.二分答案
while (l<=r){
long long mid = l+(r-l)/2,sum=0;
bool flag=false; // 用于其中一台机器满足条件时提前退出,可以帮助循环外的二分框架判断是否符合条件,相当于check函数返回的结果
for (int i=0;i<composition.size();i++){
long long totalCost = 0;
for (int j=0;j<composition[i].size();j++){
//先计算对于j种金属的数量需求
long long curDemend = composition[i][j]*mid;
if (curDemend>stock[j]){
totalCost+=(curDemend-stock[j])*cost[j];
}
}
if (totalCost<=budget){
flag=true;
break;
}
}
if (flag){
ans = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return ans;
}
};来看第四题:2071. 你可以安排的最多任务数目,先看题。
如果不会,看题解。
正如我上面所说:这题是典型的贪心,用最强的k个工人去做最简单的k个任务,最好不嗑药就能做掉最简单的任务,实在不行要嗑药就做嗑药后能做的最难任务。贪心逻辑好理解,代码实际的实现略有难度。
题解在代码的实现中,十分巧妙的运用了双端队列这个数据结构(c++中是deque,python中是collections.deque,go中只能使用切片模拟)。将一个指针独立外置,然后将嗑药能完成的任务从小到大加入这个队列,退出循环时指针自动就停在了下一次可以开始的位置。如果要嗑药就取出队尾,如果正常弄就取出队首。并且队列可以一直循环使用,只需要一直取队首和队尾就行了,十分的巧妙。如果没想到这个结构(我刚看完题解思路准备去写的时候就没想到这个结构),只能尝试使用遍历等方法,这样不但写起来麻烦,时间复杂度也会上升一个等级。
class Solution {
public:
bool check(int k,vector<int>& tasks, vector<int>& workers, int pills, int strength){
int m=workers.size(),j=0;
deque<int> q;
for (int i=m-k;i<m;i++){
//将这个工人能做的所有任务(包括嗑药)加入队列
while (j<k && tasks[j]<=workers[i]+strength){
q.push_back(tasks[j]);
j++;
}
if (q.empty()) return false; //在访问队列之前务必检查是否空 如果此处为空 说明这个工人没有能做的任务
if (q.front()<=workers[i]){ //不嗑药能做最简单的任务
q.pop_front();
}else if (pills>0){ //还有剩下的药,那就嗑药
q.pop_back(); //然后做能做的最难的任务
pills--;
}else{
return false;
}
}
return true;
}
int maxTaskAssign(vector<int>& tasks, vector<int>& workers, int pills, int strength) {
//1.排序
sort(tasks.begin(),tasks.end());
sort(workers.begin(),workers.end());
int l=0,r=min(tasks.size(),workers.size()),ans=0;
while (l<=r){
int mid = l+(r-l)/2;
if (check(mid,tasks,workers,pills,strength)){
ans = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return ans;
}
};最后,我们来到了地狱难度。第五题:2141. 同时运行 N 台电脑的最长时间,先看题。
如果不会,看题解。
这题的核心在于理解题解中当 n⋅x≤sum 成立时,必然可以让 n 台电脑同时运行 x 分钟。这句话。我的语言表达能力并不是很好,在我表达我的看法之前,先让最新的GPT-5帮我解读一下:
这题的核心想法很简单:把“允许换电池”的灵活性,等价成“可以把所有电池的电量像水一样切分并串起来使用”,但注意每块电池在同一时刻只能供给一台电脑。这就引出了一个非常干脆的判定条件。
一、把判定条件说清楚
- 如果我们打算让 n 台电脑同时运行 x 分钟,那么任何一块电池最多只能贡献 x 分钟(电量超过 x 的部分在这次目标里用不上,相当于被“截断”)。
- 因此所有电池最多能贡献的总“有效电量”是 sum(min(bi, x))。
- 想要 n 台电脑各跑 x 分钟,总需求是 n·x。
- 必要条件:sum(min(bi, x)) ≥ n·x。没有这么多“有效电量”,肯定不可能。
二、为什么这个条件也是充分的(关键点)
把电池按是否 ≥ x 分两类来构造一个可行的调度(只需说明存在性,不要求真的输出过程):1) 大电池(bi ≥ x)
- 每块这样的电池可以独立给一台电脑供满 x 分钟。
- 把它们一一分给不同的电脑,这样“占满”的电脑不再需要其他电池。
2) 小电池(bi < x)
- 设大电池用了 k 台电脑,还剩 n' = n − k 台电脑没满。
- 把剩下所有小电池(它们的总和记作 sum')串起来给这 n' 台电脑:给第 1 台从一堆小电池中接一块用完再换下一块,直到累计到 x 分钟;再给第 2 台如法炮制……依次类推。
- 这种“串电池”的方式不会出现“同一时刻同一电池被两台电脑同时用”的问题,因为每块小电池本身耗尽前持续供电时间 < x,我们可以把任何“一个电池同时贡献给两台电脑”的时间段,向时间轴两端推移为“先贡献给前一台的末尾、再贡献给后一台的开头”,从而避免重叠。
- 数学上,有 sum' = sum(min(bi, x)) − k·x。由 sum(min(bi, x)) ≥ n·x 可得 sum' ≥ n'·x。小电池总量足以把剩下的 n' 台电脑也各补到 x 分钟。
这就证明了:只要 sum(min(bi, x)) ≥ n·x,就一定能排出一个不同时共享同一电池的调度,让 n 台电脑同时运行 x 分钟。充分性成立。
三、因此可以二分答案
- 单调性:如果能同时跑 x 分钟,那一定能跑更短的时间,所以“可行时间”关于 x 是单调的。
- 二分检查:给定 x,检查 sum(min(bi, x)) ≥ n·x 是否成立即可。
边界:
- 左边界 l=0 一定可行。
- 右边界 r=⌊sum(batteries)/n⌋+1 一定不可行(因为即使用上全部电量,平均每台也撑不到 r)。
- 用开区间二分保持不变式:“l 可行,r 不可行”,直到收敛。
四、用样例直观验证
示例1:n=2, batteries=[3,3,3]
- 试 x=4:sum(min(3,4))*3=9,n·x=8,9≥8 成立,所以 4 可行。
- 试 x=5:sum(min(3,5))*3=9,n·x=10,不成立,所以 5 不可行。
- 最大可行是 4。
示例2:n=2, batteries=[1,1,1,1]
- 试 x=2:sum(min(1,2))*4=4,n·x=4,成立。
- 试 x=3:sum=4,n·x=6,不成立。
- 最大可行是 2。
五、实现要点与复杂度
- 判定函数就是一次线性遍历:累加 min(bi, x),检查是否 ≥ n·x。
- Python 代码里用 sum(batteries)//n+1 做右边界,二分时每步 O(m),总复杂度 O(m log U),U≈sum/n。
- 其他语言注意用 64 位整型承载求和与乘法,避免溢出。
六、把题解里“难点句子”翻译成直白话
- “每个电池的使用时间至多为 min(bi, x)”:因为我们只关心是否能撑到 x 分钟,多出来的电量对这次目标无用,直接“截掉”不影响可行性判断。
- “小电池串起来供电不会冲突”:因为每块小电池自身供电时长 < x,把它对两台电脑的供电安排成先后相接的时间段即可,不会出现同一时刻一电池供两台电脑。
- “sum' ≥ n'·x 就能补满剩下的电脑”:既然总小电池量足够,就可以按“用完一块换下一块”的方式逐台凑到 x 分钟。
这就是这道题的核心逻辑:把“换电池”的灵活性抽象为“截断+串接”的可分配模型,判定式 sum(min(bi, x)) ≥ n·x 既必要也充分,从而用二分搜索到最大 x。
它讲的已经非常明白了。我再来一句话概括:这个解法的核心就是,我就用x分钟,那么n台机器需要的总电量就是nx,再将每个电池真正能利用的电量累加起来,如果比它大,那就可以同时运行x分钟。除此之外不管别的。
看懂题解后,其实实行起来不难。因为我只需要计算一个式子,我们讲这么多主要是为了理解为啥这个式子是对的。
class Solution {
public:
long long maxRunTime(int n, vector<int>& batteries) {
long long l=1,ave=0;
for (auto x:batteries) ave+=x;
ave/=n;
long long r=ave+1,ans=0;
while (l<=r){
long long mid = l+(r-l)/2,sum=0;
for (auto x:batteries) sum+=min((long long)x,mid); //按照题解的思路来计算有效总电量
if (mid*n<=sum){ //按照题解的式子来判断
ans = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return ans;
}
};4.3 求间接值 0908更新
这种类型题目的核心就是,不直接二分答案,而是去直接二分和答案有相近关系的值。

这次的题目不多,难度都是中等,第二题比第一题略难,我将一一讲解。
先看第一题:3143. 正方形中的最多点数。
这题看似要求的是点数,实则这个点分布在二维空间中,并不方便量化。我们可以转而去二分正方形的边离中心点(0,0)的距离:这个距离越长,进来的点越多,越容易出现重复的点,并且这个距离和点的数量有不减的关系,并且有单调性,可以二分。
至于如何判断是否出现重复,直接使用map映射自动去重,并对比map长度和点的个数即可。
class Solution {
public:
int maxPointsInsideSquare(vector<vector<int>>& points, string s) {
int maxXorY=0; //开局找上下界
for (auto x:points){
for (auto y:x) maxXorY=max(maxXorY,abs(y));
}
int l=0,r=maxXorY,ans=0;
while (l<=r){
int mid = l+(r-l)/2,cnt=0;
map<char,int> hash;
for (int i=0;i<points.size();i++){
if (abs(points[i][0])<=mid && abs(points[i][1])<=mid){ //在正方形范围内
hash[s[i]]++;
cnt++;
}
}
if (hash.size()<cnt){ //如果哈希长度小于点的个数
r = mid-1; //说明重复,我要缩小正方形,才能更容易接近答案
}else{
ans = cnt; //记下答案
l = mid+1; //去扩大正方形
}
}
return ans;
}
};接着看第二题:1648. 销售价值减少的颜色球。
这题比较有难度,是贪心和二分的结合。如果不会做,可以先看提示,再看题解。题解可能难以理解,下面是经过GPT-5详细解读后的题解的思路:
下面我分几个层次来帮你彻底吃透这份题解与算法思想:
一、题意再精炼理解
有若干颜色的球,每种颜色 i 初始有 inventory[i] 个。顾客买球(总共 orders 个),某种颜色当前还剩 c 个时,再买走 1 个该颜色球的价值 = c。也就是:对某个颜色的库存 a,当我们依次卖出它,会得到的价值序列是 a, a-1, a-2, ..., 1。
想要最大化总价值 => 永远优先卖“当前剩余最多的那堆”的球(贪心直觉)。所以本质是在不断从“最高的柱子”削减。
但是直接用一个最大堆每次取最高值卖 1 个会超时(orders 可达 1e9)。需要“批量”卖。
二、关键贪心结构化:把所有颜色“削平”到某个高度 k
设最终我们找到一个阈值 k,满足:
- 所有初始高度 > k 的部分(也就是每堆从高度 x 降到 k)都被完全卖掉。
- 还需要再卖一些价值为 k 的球(来自那些原本 ≥ k 的堆),数量可能是 0 到某个余量。
为什么这样的结构一定存在并且是最优?
- 因为如果有一颗价值 > k 的球没卖,却卖了价值 = k 的球,这是不可能是最优的(可交换 argument)。
- 所以最优解中,卖出的球的价值集合形状:从某个最大值一路“密集”下到 k+1 全部卖出,再在 k 这个价位卖出一部分。
于是问题转化为:找到一个最小的 k,使得“所有 > k 的层” 的球数总和 ≤ orders,而“所有 > k-1 的层” 的球数总和 > orders。
也就是:
sum(max(0, x - k)) ≤ orders
sum(max(0, x - (k-1))) > orders三、二分 k 的单调性依据
定义 f(k) = sum(max(0, x - k)),表示如果把所有高度 > k 的柱子削到 k,需要卖出的球数。
显然:
- k 越大,每个 (x - k) 越小 => f(k) 单调不增。
- 我们想找“最小的 k,使 f(k) ≤ orders”。这就是典型的单调条件二分。
代码里:
l = 0, r = max(inventory)
mid = (l + r)>>1
s = f(mid)
如果 s > orders,说明削到 mid 仍用掉太多球(比允许卖的多),要“削少一点” => 即提高 k(l = mid + 1)
否则 s ≤ orders,说明 k 还可以再小一点(让价值更高) => r = mid - 1
循环后 l 即所求最小 k。四、找到了 k 之后如何算答案
- 先把所有 x > k 的柱子从 x 一路卖到 k+1。
这一段对单个柱子贡献的价值:
x + (x-1) + ... + (k+1)
是一个等差数列,项数 = x - k
和 = ( (x) + (k+1) ) * (x - k) / 2
= (x + k + 1)*(x - k)/2- 上面这些全部卖出后,卖掉的总数量 sold_high = sum(x - k for x>k)
- 还需要卖 rest = orders - sold_high 个价值 = k 的球(这些来自那些原本 ≥ k 的堆,数量肯定够,因为如果不够,k 就不会是二分得到的最小满足值)。
- 答案 = 高于 k 的那些“梯形块”总和 + rest * k
- 最后取 mod。
五、代码里几个容易迷惑的点
- 为什么最终 k = l 而不是 r?
因为我们找的是“最小使 f(k) ≤ orders 的 k”,典型的“下界”二分模板,循环结束时 l 指向第一个满足条件的位置。- 为什么 sum 用的是 x - mid 而不是 (mid - x)?
因为只对 x > mid 的堆需要削减,削掉的层数正是 x - mid,每层一个球。- 为什么计算 rest 时再次用 sum(x - k for x>k)?
因为 sold_high 是真正卖掉的“价值 > k”球的数量;不能用 mid 版本的 s(因为 mid 最终不是 k,k 是二分后的 l)。- range_sum(k+1, x) 的推导:
range_sum(a, b) = (a + b)*(b - a + 1)/2
这里 a = k+1, b = x
=> (k+1 + x) (x - (k+1) + 1)/2 = (k+1 + x)(x - k)/2 = (x + k + 1)*(x - k)/2
与注释一致。- 为什么要“k 尽可能小”?
因为 f(k) ≤ orders 保证能卖足 orders 个球;在满足数量的所有 k 中,k 越小说明我们越多地使用了高价值层(等差数列的起点更高),总价值自然更大。六、用一个具体例子手动演示(inventory = [2,5], orders = 4)
inventory = [2,5], 最大 5
试 mid:
mid=2: f(2) = (5-2)=3 ≤ 4 => r = 1 (想再小一点)
mid=0: f(0) = (2-0)+(5-0)=7 > 4 => l = 1
mid=1: f(1) = (2-1)+(5-1)=1+4=5 > 4 => l = 2
循环结束: l=2 => k=2
sold_high = sum(x - 2 for x>2) = (5-2)=3
rest = 4 - 3 = 1
高层收益:从 5 降到 3 的价值 5+4+3 = 12
rest=1 个价值 = k = 2 的球 => 12 + 2 = 14七、复杂度分析
- 二分次数:log(max(inventory[i])),最大约 log(1e9) ≈ 30
- 每次二分内做一次 O(n) 遍历 => 总 O(n log M),n ≤ 1e5,可接受。
- 空间 O(1) 额外。
八、可能的优化 / 其他思路
排序 + 分层批量卖(不需要二分):
- 将库存排序,从最大往下,与次大之间的“高度差”乘以“有多少堆达到这个高度”就是可批量卖的层数。
- 类似“削峰”法,一层层大块卖,直到 orders 用完。
- 每次处理一段高度区间,利用等差数列一次结算。
- 复杂度 O(n log n) 或 O(n)(如果用计数结构)。
最大堆 + 批次:
- 取最大值 c 和次大值 d(若不存在则 d=0),可以一次性卖 min(orders, c - d) 层。
- 但每次需要 log n 调整堆,仍然可行,但实现较繁琐。
- 本题所用“二分 k”法思路清晰,代码简洁,是常见高频写法。
九、常见易错点
- 把等差求和上/下限写错(注意是卖到 k+1 停)。
- rest 计算用错(要用最终 k 重新算)。
- 没有用 long / Python int(在别的语言里可能溢出)。
- 忘记取模或在中间取模导致负面影响(本题可最后统一取模)。
十、代码再加详细注释版本
class Solution: def maxProfit(self, inventory, orders): mod = 10**9 + 7 # 二分找最小 k 使得 sum(max(0, x - k)) <= orders l, r = 0, max(inventory) while l <= r: mid = (l + r) >> 1 s = 0 # 计算把所有 > mid 的堆削到 mid 需要卖多少球 for x in inventory: if x > mid: s += x - mid if s > orders: # mid 太小,削掉的数量太多,提升 k l = mid + 1 else: # mid 可以满足,尝试更小 r = mid - 1 k = l # 最小可行阈值 # 先统计“价值 > k”的那些球的总数(已经确定全卖掉) sold_high = 0 ans = 0 for x in inventory: if x > k: cnt = x - k # 卖出的数量(层数) sold_high += cnt # 卖出的价值:x + (x-1) + ... + (k+1) # 等差数列和 = (首 + 尾) * 项数 / 2 ans += (x + (k + 1)) * cnt // 2 # 还需要从价值 == k 的层卖 rest 个 rest = orders - sold_high ans += rest * k return ans % mod十一、如何直觉理解“让 k 越小越好”
假设存在两个可行阈值 k1 < k2,且都满足 sum(max(0, x - k)) ≤ orders。
- 使用 k2 的方案:你卖掉所有高于 k2 的层 + 一些 k2 层。
- 如果改成 k1:你会多卖掉一些更高价值的层(介于 k1+1 和 k2 之间),而少卖一些价值较低的 k2 层或 k1 层。
- 总价值一定不降。
所以要最小的可行 k。十二、与优先队列贪心的等价性
优先队列写法等价于“每次取最高的柱子往下砍”,二分法则是把这个过程整体“压缩”,直接找到最终平衡点 k,再一次性结算各段高度贡献。
十三、总结一句话
通过二分确定“最终统一削到的高度 k”,把所有比 k 高的部分整段算等差数列,剩下不够的再用 k 补齐,数学求和 + 模即可。
如果你还想看“分层批量卖”的另一种实现方式,或想让我对比两种写法的具体操作步骤,也可以继续问我。
如果上面某一段还有不清晰的地方,告诉我你卡在哪里,我再针对性补充。
AI讲的真的很不错。我就不补充了。下面是我的ac代码:
class Solution {
public:
int maxProfit(vector<int>& inventory, int orders) {
//1.找上下限
long long l=0,r=0,mod=1000000007,ans=0;
for (auto x:inventory) r = max(r,(long long)x);
while (l<=r){
long long mid = l+(r-l)/2,cnt=0;
__int128_t sum=0; //开int128防止溢出
for (int i=0;i<inventory.size();i++){
if (inventory[i]>=mid){
cnt+=inventory[i]-mid; //我这里的思路和题解略有不同,我是在二分里面直接就算钱了
sum+=(__int128_t)(mid+1+inventory[i])*(__int128_t)(inventory[i]-mid)/2;
}
}
if (cnt>orders){
l = mid+1;
}else{
sum += (orders-cnt)*mid;
ans = sum;
r = mid-1;
}
}
return ans%mod;
}
};4.4 最小化最大值 0924更新
4.4.1 简介
经过两个星期的艰难前行,经历各种大大小小的事情,在开学后我刷题的时间比暑假在家减少了一些。前些天刚刚去考了第39次ccf csp认证,也是喜提当次前7%的好成绩(比我上次前60%进步了53%,高于我们实验班大三上结束之前达到前30%的硬性要求),也是终于可以专心准备面试算法了。
那么在开始讲解题目之前,我先来讲讲:啥是最小化最大值?
你可以理解成,我二分出来的mid是上界,然后我在check的过程中,确保经过某种处理后,所有元素都不超过mid这个上界,如果符合,我就再把mid通过二分压低;如果不符合则反之。这就是最小化最大值。
下面的图片讲的也很形象:好比用一个盖子压住最大值,看看能不能压住。

为何有些题目我没做呢?像2064这种题目,就是没学习到相关数据结构的知识;3399和3605则是我连题解也无法理解,也是缺乏相关知识的学习。后续如果学习到了相关知识,有机会的话,会回来补的(可能优先去做hot100了也有可能)。
下面是我本人对本次题目的主观上的难度排序:
1.基础题(我能较快做出来)
没有
2.进阶题(我需要思考一下才能做出来)
410. 分割数组的最大值 最小化最大值题型的入门题,是第一道门槛
1631. 最小体力消耗路径 1948 结合BFS考察,需要想到:如果差值大于mid就将其当成无法跨越的障碍,然后BFS寻路看能否到达终点
(讲解)1760. 袋子里最少数目的球 1940 需要想到用除法运算来算出分隔操作的次数,并且正确处理能/不能整除的场景
2064. 分配给商店的最多商品的最小值 1886 和1760思路类似,使用向上取整的整除来算出这一批商品能分到的店的数量,最后和实际店铺数量对比
(讲解)2560. 打家劫舍 IV 2081 考察01-DP,只偷金额小于等于mid的房间,使用dp记录当前偷取的房间数量,最终和k对比得出结论
(讲解)778. 水位上升的泳池中游泳 2097 考察BFS,由于可以瞬时无限移动,所以只需要等mid秒后再出发即可,将大于mid的格子作为障碍
3.困难题(大体思路正确,但是需要纠正一些细节后才能做对)
2439. 最小化数组中的最大值 1965 这题需要想到,加一减一的操作本质上就是将后面的超出mid的数全部向前堆积到下标0的位置,只需要判断下标0位置的元素最终是否<=mid即可
(讲一些注意的点)2616. 最小化数对的最大差值 2155 总体思路就是先排序,取前后相邻的下标,然后使用哈希记录使用过的下标,然后判断是否取够了数量
(讲解)3419. 图的最大边权的最小值 2243 考察BFS和反图,先构造反图,然后bfs时不经过大于mid的边权,看能否访问到全部节点。这题力扣还会卡我时间
4.地狱题(我看了题解还得理解很久,才能彻底弄懂)
(一笔带过)2513. 最小化两个数组中的最大值 2302 纯纯的数学题目,需要掌握辗转相除法
(讲解)LCP 12. 小张刷题计划 用贪心的思路将当前区间内最耗时间的题目交给小刘解决,然后还得处理天数的边界
5.78题(题解里面需要用到我目前没掌握的,且难以快速掌握的知识解决题目,所以看了题解也无法做出)
3613. 最小化连通分量的最大成本 约 1900 涉及并查集相关知识点,我尚未学习到
3399. 字符相同的最短子字符串 II 2376 题解使用了最大堆/分桶优化,比较难以理解
3399. 字符相同的最短子字符串 II 2376 题解使用了LogTrick / 栈,比较难以理解
4.4.2 开始讲解!
首先来到本次讲解的第一题:1760. 袋子里最少数目的球,先看题。
提取题目要素:你的开销是单个袋子里球数目的 最大值 ,你想要 最小化 开销。这是最大化最小值的特征。
首先,看到题目的第一想法,肯定是用循环模拟将球一个一个放进去。但是这样时间复杂度会爆炸,所以转而很容易会想到用除法来计算这一种类的球需要分隔几次才能低于mid:cnt += nums[i] / mid;。
满怀期待去运行,结果直接答案错误——漏考虑了mid能把nums[i]整除的情况。
如果能整除,那么操作的次数就需要-1(例如把6分割成3和3,6/3=2,但是实际只需要分割一次),也就是:cnt += nums[i] / mid - 1;。
至此,题目的具体逻辑就是这样的。
class Solution {
public:
int minimumSize(vector<int> &nums, int maxOperations) {
int l = 1, r = nums[0], ans = 0;
for (auto x: nums) r = max(r, x);
while (l <= r) {
int mid = l + (r - l) / 2; //每份球的数量
long long cnt = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > mid) {
if (nums[i] % mid == 0) { //如果能整除
cnt += nums[i] / mid - 1;
} else { //如果不能
cnt += nums[i] / mid;
}
}
}
if (cnt > maxOperations) { //如果分隔的总次数比允许的最多操作次数多
//说明压的太低了
l = mid + 1;
} else {
r = mid - 1;
ans = mid;
}
}
return ans;
}
};接下来来到第二题:2560. 打家劫舍 IV,先看题。
从这里开始,我就基本不会讲二分了,只讲如何实现check()函数。
好好好久不见的DP也是终于返厂了。
先看题目要素:小偷 不会窃取相邻的房屋->使用DP,在每一步操作分类讨论偷还是不偷,并将结果一直传递下去;
窃取能力是能从单间房屋中窃取的 最大金额,需要返回小偷的 最小 窃取能力 ->最小化最大值。
那么该如何使用DP呢?我们建立一个二维数组dp[n][2]来存储小偷偷的房间数量,其中dp[i][0]表示不偷这间房屋,dp[i][1]表示偷这间房屋。
根据题意,小偷不能偷相邻的两间房屋,所以如果他偷了上一间房屋,这一间房屋就不能偷。因此,这一间房屋如果要偷,物品价值必须<=mid,确保压住物品金额的上限,并且只能继承上一间房屋没偷的状态,也就是dp[i][1]=dp[i-1][0]+1;如果不偷这间房屋,那么上一间房子偷不偷都行,为了确保小偷偷的房间数量尽量多(需要>=k),直接选择继承上一个房间的最大值就行,即dp[i][0]=max(dp[i-1][0],dp[i-1][1])。
题目基本的逻辑就是这样,见代码:
class Solution {
public:
bool ok(vector<int> nums, int mid, int k) {
vector<vector<int> > dp(nums.size(), vector<int>(2, 0));
//初始值必须是0,因为下面如果偷不了某个房间,会直接忽视dp[i][1]
if (nums[0] <= mid) dp[0][1] = 1;
for (int i = 1; i < nums.size(); i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]); //如果本次不偷
if (nums[i] <= mid) dp[i][1] = dp[i - 1][0] + 1; //如果本次偷,物品的价值必须<=mid,确保压住上限
}
if (max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]) >= k) return true;//如果最终偷到的房间数量达到了k
return false;
}
int minCapability(vector<int> &nums, int k) {
int l = nums[0], r = nums[0], ans = 0;
for (auto x: nums) {
l = min(l, x);
r = max(r, x);
}
while (l <= r) {
int mid = l + (r - l) / 2;
if (ok(nums, mid, k)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
};接下来来看第三题:778. 水位上升的泳池中游泳,先看题。
提取要素:走格子->bfs/dfs;
每个格子在特定时间后解锁->时间越往后越容易走通->时间需要能压住路径上的时间的最大值->要求时间最短->最小化最大值。
所以这题,如果你是单独刷到,不是这一系列题目的连贯练习,可能想到用最小化最大值去做比较有难度。怪不得我感觉这题目做着不难,却是hard水平。
这时候就能体现二分查找的魅力时刻了:正向去做需要用到堆和并查集的知识,而二分查找只需要直接去猜时间是多少,然后用bfs去验证是否可达就行了。
题目有一个很关键的条件:假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。
这说明,我可以放心去猜时间,放心去bfs,因为只要当前猜测的时间下,路径通了,就能到达。
所以思路明了了:猜一个时间,然后将时间大于mid的方块当成障碍,去bfs/dfs判断是否能到达终点即可。
这里我用的是bfs,因为不是很喜欢写递归。bfs还不会的可以移步我的另一个算法笔记。
class Solution {
public:
bool canReach(vector<vector<int> > &grid, int time) {
vector<int> dx = {-1, 1, 0, 0}, dy = {0, 0, -1, 1};
int n = grid.size();
queue<pair<int, int> > q;
vector<vector<int> > dist(n, vector<int>(n, -1));
q.emplace(0, 0);
dist[0][0] = 0;
while (!q.empty()) {
//取出队首
auto [x,y] = q.front();
q.pop();
if (x == n - 1 && y == n - 1) {
return true;
}
for (int d = 0; d < 4; d++) {
int nx = x + dx[d];
int ny = y + dy[d];
//检查合法性
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
//将大于当前时间的格子当成障碍
if (dist[nx][ny] != -1 || grid[nx][ny] > time) continue;
//合法,加入队列接着扩散
q.emplace(nx, ny);
dist[nx][ny] = dist[x][y] + 1;
}
}
if (dist[n - 1][n - 1] != -1) return true;
return false;
}
int swimInWater(vector<vector<int> > &grid) {
int n = grid.size(), ans = -1;
int l = max(grid[n - 1][n - 1], grid[0][0]), r = 0;
for (auto x: grid) {
for (auto y: x) {
r = max(r, y);
}
}
while (l <= r) {
int mid = l + (r - l) / 2;
if (canReach(grid, mid)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
};
这下真是二分查找魅力时刻了:二分+某基础算法,能创造很多可能。
我们接着来第四题:2616. 最小化数对的最大差值,先看题。
先讲一讲思路:将数组排序,这样两个相邻的元素一定是差值最少的,然后二分猜值,如果当前相邻元素没取过,并且差值<=mid,则计数器加一,将这两个元素的下标放入哈希表中,用于去重。
这个哈希表在cpp中是啥呢?是map吗?不是。map是基于红黑树实现的,查询的时间复杂度需要O(logn)。
真正的哈希表是以unordered_开头的容器,详情见下表:
| 容器名 | 类型 | 底层原理 | 插入/删除 | 查找 | 访问最小/最大 | 备注 |
|---|---|---|---|---|---|---|
| std::set | 集合 | 红黑树(平衡二叉树) | O(log n) | O(log n) | O(log n) | 自动排序,唯一 |
| std::unordered_set | 集合 | 哈希表 | O(1) | O(1) | 不支持 | 无序,唯一 |
| std::multiset | 集合 | 红黑树(平衡二叉树) | O(log n) | O(log n) | O(log n) | 自动排序,可重复 |
| std::unordered_multiset | 集合 | 哈希表 | O(1) | O(1) | 不支持 | 无序,可重复 |
| std::map | 映射 | 红黑树(平衡二叉树) | O(log n) | O(log n) | O(log n) | 自动排序,唯一键 |
| std::unordered_map | 映射 | 哈希表 | O(1) | O(1) | 不支持 | 无序,唯一键 |
| std::multimap | 映射 | 红黑树(平衡二叉树) | O(log n) | O(log n) | O(log n) | 自动排序,可重复键 |
| std::unordered_multimap | 映射 | 哈希表 | O(1) | O(1) | 不支持 | 无序,可重复键 |
所以为啥我会突然提起这个呢?因为这道题,我第一次提交的时候,我使用map来去重,结果超时了。询问ai后,我改成了unordered_set,直接不超时了。最根本的原因是:前者访问元素的时间复杂度为O(logn),而后者是O(1)。
贴一下ac代码:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool ok(vector<int> nums, int mid, int p) {
unordered_set<int> used; //这里使用无序集合去重,访问的时间复杂度O(1)
int cnt = 0;
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] - nums[i] <= mid && used.count(i + 1) == 0 && used.count(i) == 0) {
cnt++;
used.emplace(i + 1);
used.emplace(i);
}
}
return cnt >= p;
}
int minimizeMax(vector<int> &nums, int p) {
int l = 0, r = 0, ans = -1;
sort(nums.begin(), nums.end());
r = nums[nums.size() - 1] - nums[0];
while (l <= r) {
int mid = l + (r - l) / 2;
if (ok(nums, mid, p)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
};
接下来来看第五题:3419. 图的最大边权的最小值,先看题。
要素提取:
最大边权的最小值->最小化最大值;
所有其他节点都可以到达节点 0 ->搜索(bfs/dfs)。
刚刚看到题目,我就有个疑问:这个threshold有啥用?我操作是只会删边,不会增边的,限制我这个干啥?
直觉告诉我,我不需要管这个,后来在做完题目后,也证实了:确实是个多余的条件。在后面我会分析为什么。
好了,接着着手题目本身。它要求最大边权值尽可能小,说明我得二分一个mid,然后把>mid的边都删除了,然后再判断是否所有节点都能到达0节点。结果超时。
好的,进行第一波优化:删除边(erase)的操作时间复杂度O(n),太慢了。于是,我改成直接访问这个图,不走>mid的边。结果还是超时。
然后,第二波优化:判断所有点能否到0太慢了,得先做反图(将原图a->b的关系全部改成b->a),然后从0开始bfs,判断是否经过了所有节点,这样能快一个数量级。结果还是超时。
没招了,我问ai,ai说:
你这版 TLE 的最大元凶是这个函数签名: bool check(vector<vector<vector
> > rev, int mid, int n) 这里把 rev 按值传递了!每次二分 check 都会把整张反图深拷贝一遍(外层 vector 拷贝、每个邻接表 vector 拷贝、每条边的小 vector
{to,w} 也拷贝)。这直接把每次检查从 O(V+E) 拉到 O(V+E) + O(E) 的大常数,数据大时必超时。
行,第三遍优化:我把函数头部加上static const,变量传递也全部都是引用传递,避免拷贝,然后把原本的三维数组改成了更轻量的以pair<int,int>为基的二维数据。终于通过了。sb力扣我漕你冯福

经过这么一番折腾,我们可以总结出这道题目的做法:mid猜边的最大值,然后制作反图,从0开始做无目标的bfs,不走>mid的边,看看能否经过所有节点。只有这个反图的优化我认同,其他的我都不认同,纯纯评测系统故意卡的。
来看我精装修后的代码:
class Solution {
public:
static bool check(const vector<vector<pair<int, int> > > &rev, const int mid, const int n) {
vector<bool> used(n, false);
queue<int> q;
q.emplace(0);
used[0] = true; //记录是否使用过
int seen = 1;
while (!q.empty()) {
//先取出队首
int cur = q.front();
q.pop();
//由于是无目标bfs,所以这里不需要检验是否到终点
//等全部能访问的节点都访问完之后,队列自然会空,bfs自然会停止
for (auto newNode: rev[cur]) {
if (used[newNode.first] || newNode.second > mid) continue;
q.emplace(newNode.first);
used[newNode.first] = true;
seen++;
if (seen == n) return true;
}
}
return seen == n;
}
int minMaxWeight(int n, vector<vector<int> > &edges, int threshold) {
//1.先构建反图
vector<vector<pair<int, int> > > rev(n, vector<pair<int, int> >());
for (int i = 0; i < edges.size(); i++) {
rev[edges[i][1]].emplace_back(edges[i][0], edges[i][2]);
}
//2.开始二分
int l = edges[0][2], r = l, ans = -1;
for (const auto x: edges) {
l = min(l, x[2]);
r = max(r, x[2]);
}
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(rev, mid, n)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
};
最后来讲讲为啥不需要管threshold。我们这道题对于边权的追求是越小越好,而我们的追求越小,被删除的边就会越多,这样就越能符合threshold的条件。如果我删除到无法联通的情况下,threshold还是不达标,说明这个用例是无赖用例,没有任何意义。所以,最好的办法就是不管这个threshold,这是合理的。
接着,我们来讲第六题:LCP 12. 小张刷题计划,先看题。
要素提取:每天的做题时间中耗时最多的是T->求最小的T->最小化最大值。
并且题目里面有一个机制:每天小张可以挑选任意一道题目找小刘解决,相当于直接减去这道题目的时间。所以,从贪心的角度,我们能很容易想到尽量将每天最耗时间的题目给小刘做,这样才能最大程度压低每天的总时间。
这样,我们就形成了代码的雏形:二分猜每天最多的时间mid,然后for循环累加每天的题目同时维护最大值,如果总和+题目耗时最大值已经超过了mid,说明我就算给小刘做最大的题目也无法小于等于mid了,所以这一天必须得结束了,就将天数减一。超出的这个题目只能留给明天做了,所以重置累加器和最大值为当前题目耗时。
当然,由于都会有一道题目要留给明天做,所以如果天数为最后一天的时候触发了这个条件(总和+题目耗时最大值超过mid),就说明这个mid压不住了,因为已经是最后一天了,哪来新的“下一天”。这就是我在上面题目列表简介列表旁边所说的边界。
代码如下,有详细注释:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool ok(int &mid, vector<int> &time, int m) {
int sum = 0, maxTime = time[0];
for (int i = 0; i < time.size(); i++) {
sum += time[i]; //累加每道题的时间
maxTime = max(maxTime, time[i]); //维护一个做题时间的最大值
if (sum > mid + maxTime) { //如果请小刘来也没达到我们mid的要求
if (m > 1) { //如果还有“明天”
m--; //天数减一
sum = time[i]; //重置累加和为当前时间,留到明天做
maxTime = time[i]; //重置最大时间为当前时间
} else { //如果是最后一天
return false; //说明这个mid的要求不得行
}
}
}
return true;
}
int minTime(vector<int> &time, int m) {
int l = 0, r = 0, ans = -1;
for (auto x: time) r += x;
while (l <= r) {
int mid = l + (r - l) / 2;
if (ok(mid, time, m)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
};4.5 最大化最小值 1020更新
4.5.1 简介
这次的题目也是非常有难度,再加上国庆节玩了8天,这八天一天都没刷题,导致了我过了好久才软磨硬泡的把这些题目弄完。
本次做题情况如下:

和4.4一样,有一些我没做的题目是因为涉及到了更高深的知识(依旧是并查集)。只要是我现有知识能解决的题目,我都会去尝试把它做掉。
下面来分析一下本次题目的难度,划分一下讲解顺序:
1.基础题(我能较快做出来)
没有
2.进阶题(我需要思考一下才能做出来)
3281. 范围内整数的最大得分 1768 思路没啥特别的,看代码能比较容易回想起来,算是最大化最小值的入门题吧(可能略难)
2517. 礼盒的最大甜蜜度 2021 也是经典思路:排序价格,然后代入二分的答案去试是否某个糖果的价值-上个糖果的价值>=mid,然后计数器计数,最终比较这样选出来的糖果数量是否达到了要求
1552. 两球之间的磁力 同 2517 题 确实,和上面这道题思路一模一样,没啥好说的
3.困难题(大体思路正确,但是需要纠正一些细节后才能做对)
(讲解)2812. 找出最安全路径 2154 此处学习到了新知识:多源bfs。这题用了2次bfs:一次是多源bfs用于确定每个格子到最近小偷的距离,一次用于判断是否能在给定mid下到达终点
(讲解)3449. 最大化游戏分数的最小值 2748 此题极其烦人。可以当成那种现场手撕的题目,因为没啥算法可以套用。具体做法后面讲
4.地狱题(我看了题解还得理解很久,才能彻底弄懂)
(讲解)2528. 最大化城市的最小电量 2236 这题的难度还是比较地狱的。需要用前缀和来快速计算每个城市所接收到的能量,然后再用差分数据来快速更新一串城市之间的最新电量。后续思路在后面讲解。
(讲解)3464. 正方形上的点之间的最大距离 2806 此题也是私募了。有很多种解法,我一开始是做不出来的,看了题解后决定采用二分套二分的做法,然后一直做不出...最后还是借助了ai神力,修正了错误才做出来。
5.78题(题解里面需要用到我目前没掌握的,且难以快速掌握的知识解决题目,所以看了题解也无法做出)
3620. 恢复网络路径 1998 题解需要用到DAG DP / 拓扑排序 尚未学到,先不做
3600. 升级后最大生成树稳定性 2301 需要使用并查集 尚未学习
4.5.2 开始讲解
首先我们来讲解第一题:2812. 找出最安全路径,先看题。
首先,看到题目是矩阵,并且从左上角走到右下角,很难不联想到搜索算法。在搜索算法中,最通用的算是bfs(广度优先搜索)算法了,因为它既能算是否能到达某个点,又能算到达某个点的最短步数,不像dfs算法,只能算能否到达。所以我们想到了使用bfs来解决这道题目。
又因为这道题目是在二分题单里面的,带着目的想问题,我们很容易想到去二分猜这个最大安全系数,然后再代入这个安全系数到bfs中,检验是否能在全程不超过这个安全系数的前提下,走到终点。
那么现在只剩下最后一个障碍了:如何算出每一格到最近的小偷单元格的曼哈顿距离?
你肯定会首先想到去O(n^3)复杂度的遍历:外层循环用来找小偷单元格,然后内层的两个循环来给每个格子标它自己到当前选定的小偷单元格的距离,再引入min函数来取最小值,这样每一格留下的都是最短的距离。
这样的方法当然行得通,但是太慢了。我们需要更快的方法——这就是这次我们需要用到的新知识:多源bfs。
定义如下:
多源 BFS 是指从多个起始点同时开始进行广度优先搜索(BFS)。与单源 BFS 不同的是,多个起点同时进入队列,BFS 会同时向所有方向扩展。其核心思想是将多个源节点的影响同时传播到其他节点,常用于求解多源最短路径、最小距离等问题。
步骤:
- 将所有源节点入队。
- 对队列中的每个节点,进行标准的 BFS 扩展,更新相邻节点的距离或状态。
常用于计算多个点到所有其他点的最短距离(如多源最短路径问题)。
在这道题目中,我们只需要先遍历整个矩阵,然后记录下所有小偷格子的坐标,然后将它们全都丢进bfs的初始队列中,相当于以它们为起点,向四处扩散开来。接着,进行正常的bfs流程(只不过去掉了校验终点的流程,因为多源bfs一般来说是没有目的的随意遍历),再继续引入min函数,这样就能方便快捷的获得每一格到最近的小偷格子的曼哈顿距离。而且很有意思的点是,bfs的dist数组本身记录的步数就是从起点出发到此处的曼哈顿距离,所以甚至都不需要另外计算距离,直接填入步数即可。
到这里,题目的基本思路就实现完了。看代码,重点看上面两个函数:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
public:
//使用bfs判断是否能在当前安全系数下到达终点
bool canReach(vector<vector<int> > &d, int mid, int n) {
if (d[0][0] < mid || d[n - 1][n - 1] < mid) return false;
queue<pair<int, int> > q;
q.emplace(0, 0);
vector<vector<int> > dist(n, vector<int>(n, -1));
dist[0][0] = 0;
while (!q.empty()) {
auto [cx,cy] = q.front();
q.pop();
if (cx == n - 1 && cy == n - 1) {
return true;
}
for (int dir = 0; dir < 4; dir++) {
int nx = cx + dx[dir];
int ny = cy + dy[dir];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (dist[nx][ny] != -1 || d[nx][ny] < mid) continue;
q.emplace(nx, ny);
dist[nx][ny] = dist[cx][cy] + 1;
}
}
return dist[n - 1][n - 1] != -1;
}
//使用多源bfs计算每个格子到最近小偷格子的曼哈顿距离
vector<vector<int> > getDist(vector<vector<int> > &grid, int n) {
vector<vector<int> > d(n, vector<int>(n, -1));
queue<pair<int, int> > q;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) { //如果是小偷格子
q.emplace(i, j); //加入多源bfs的起始队列中
d[i][j] = 0;
}
}
}
while (!q.empty()) {
auto [x,y] = q.front();
q.pop();
//开始无目的多源bfs
for (int dir = 0; dir < 4; dir++) {
int nx = x + dx[dir];
int ny = y + dy[dir];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (d[nx][ny] == -1 || d[nx][ny] > d[x][y] + 1) {
d[nx][ny] = d[x][y] + 1;
q.emplace(nx, ny);
}
}
}
return d;
}
int maximumSafenessFactor(vector<vector<int> > &grid) {
//1.计算d
int n = grid.size();
auto d = getDist(grid, n);
//2.二分计算当前安全值下是否可达
int l = 0, r = 2 * n, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (canReach(d, mid, n)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
private:
vector<int> dx = {-1, 1, 0, 0};
vector<int> dy = {0, 0, -1, 1};
};好了,我们接着来看第二题:3449. 最大化游戏分数的最小值 ,先看题。
这道题的基本思路很简单,题目的提示里面也有写:
We should go from i to (i + 1) back and forth, making the value for each index i (from left to right) no less than x.
说白了,就是如果i的分数不够,我们就前后前后的在i和i+1之间来回横跳,直到i的分数足够了,我们才继续往下。
看完这个提示,我相信你们肯定能形成一个大概思路了:先用二分猜游戏分数的最小值,然后遍历游戏分数,如果遇到小于这个最小值的points[i],就来回横跳给它加到mid,然后再往下,记录下操作的次数。最后再比较这个操作次数是否<=m(也可以在中途放一个判断,只要大于了就break,节省时间)。
思路归思路,但是实现起来并不是一帆风顺的。
首先,你会想到:前后横跳,如果在最后一位怎么办?所以,我们需要分类讨论:如果i在最后一位,那就往前来回横跳。这只是其中一个需要判断的东西,我们还需要思考啥时候这个次数超出m的时候才应该退出?啥时候超出m的时候break?这很难用语言文字来描述,到时候我在代码旁边注释。
将上面都安排妥当后,最后还得检查是否所有的point都不小于mid。因为上面有一个次数超出m直接break的式子,触发这个式子并不一定是失败了,也有可能是完成最后一个小于mid的point的填充之后,我多跳了一下,导致次数超出。所以这时候就需要扫描一下points,来二次确认到底合格了没有。
不多说了,看代码:
using ll = long long;
class Solution {
public:
bool ok(vector<int>& points, int m,ll mid) {
vector<ll> gameScore(points.size());
ll curM = 1; //由于开局指针在-1,从-1到0是必须走一步的,所以直接初始化计数器为1
for (int p=0;p<points.size();p++) {
if (curM>m) break; //这里是应对完成最后一个i然后多走了一步超出的情况,交由下面的range循环二次检查
gameScore[p]+=points[p];
if (gameScore[p]<mid && p!=points.size()-1) { //处理i不是最后一位的情况
ll diff = mid-gameScore[p]; //计算当前分数和二分的目标分数的差距
ll time = (diff+points[p]-1)/points[p]; //用向上取整算需要加分的次数
if (time*2>m-curM) return false; //上述次数*2就是操作的次数
gameScore[p]+=time*points[p]; //给i加分
gameScore[p+1]+=time*points[p+1]; //给i+1加分(被迫营业,当然从贪心的角度来看,往后加分是最好的,不浪费操作次数)
curM+=time*2; //上述次数*2才是操作的次数(因为需要来回横跳)
}else if (gameScore[p]<mid && p==points.size()-1) { //处理i是最后一位的情况
//下面的逻辑和上面一样,就是把i+1变成了i-1而已,就不注释了
ll diff = mid-gameScore[p];
ll time = (diff+points[p]-1)/points[p];
if (time*2>m-curM) return false;
gameScore[p]+=time*points[p];
gameScore[p-1]+=time*points[p-1];
curM+=time*2;
}
curM++; //每往后移动一次次数加一
}
for (auto x:gameScore) { //这里的遍历主要是处理break出来的情况,用于二次确认
if (x<mid) return false;
//因为有可能我已经把最后一个i给加到了mid,不需要再移动了,但是我的程序默认是移动偶数次数,所以就有可能刚好超出一次次数。这种情况应该是被允许的
}
return true;
}
long long maxScore(vector<int>& points, int m) {
ll l = 0,r = points[0],ans = -1;
for (auto x:points) r = max(r,(ll)x);
r*=m;
while (l<=r) {
ll mid = l+(r-l)/2;
if (ok(points,m,mid)) {
ans = mid;
l = mid+1;
}else {
r = mid-1;
}
}
return ans;
}
};好了,我们接着来看第三题:2528. 最大化城市的最小电量,先看题。
题目“供电”的定义很简单:供电站给自己r距离范围内的城市供电,被波及到的城市获得1个电量,然后叠加。
所以,为了计算出城市i的电量,我们需要获得这个城市[i-r,i+r]范围内的供电站数量,而累加这个操作,相当于计算[i-r,i+r]范围内的区间和,我们能很容易想到前缀和。所以,我们的第一步是用题目提供的stations供电站数量数组,来构建一个供电站数量的前缀和数组。这样,我们在计算每个城市的电量(即[i-r,i+r]的区间和)时,只需要O(1)时间复杂度,十分快速。
好了,接着我们需要将这道题目代入二分算法的逻辑。我们选择二分答案,而这个答案就是所有城市电量的最小值,然后我们又能新建供电站k座。以往的做题思路告诉我们,我们需要先二分一个mid,然后再遍历每个城市的power,如果这个power<mid,那就需要新建供电站。那么,这个供电站应该建在哪里呢?和上道题目的反复横跳有些类似,用贪心的思路判断,我们应该建供电站在这个城市的后面,正好使这个城市在供电站所能波及到的边界就行。因为如果建供电站在这个城市的前面,或者新建的供电站能波及到这个城市左边的城市,电力资源就存在了浪费:这个城市左边的城市的电量是很明显>=mid,但是这个城市右边可能会存在城市的电量<mid,如果供电站位置偏左,导致右边那个城市正好在这个新建供电站的波及范围之外,这不是浪费资源了吗。所以,将这个城市处于新建供电站的波及范围的左边界是最优解。当然,注意一下别超出城市数组的右边界了,这里就需要用到一个max。即:将供电站放在max(数组右边界,i+r)的位置。
那么在新建供电站之后,我们需要更新所波及到的所有城市的电量,相当于一个一个的更新区间和。那么我们该如何快速更新呢?这时候就需要用到差分数组了。我们构建一个差分数组,然后利用差分数组的当前元素值即为其前序元素之和的特性,一直累加维护一个变量cur,就可以直接获取当前城市的真实电量,然后再进入上面的判断逻辑,若电量<mid就新增供电站,使用差分数组快速更新区间上每一个城市的电量。
思路到这里就讲完了,下面看代码,有详细注释:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
public:
bool ok(vector<ll> &power, int r, ll k, ll mid, int n) {
vector<ll> diff(n, 0); //初始化差分数组
ll used = 0, cur = 0; //used是记录新建电站的机会使用次数,cur表示当前城市电量
diff[0] = power[0];
//构建差分数组
for (int i = 1; i < n; i++) {
diff[i] = power[i] - power[i - 1];
}
for (int i = 0; i < n; i++) {
cur += diff[i]; //累加维护当前城市电量
if (cur < mid) { //若当前城市电量没达到mid
ll m = mid - cur; //计算出需要新建电站的数量
used += m; //记录下来
if (used > k) return false; //如果使用的机会数量超过了k次,说明失败了,就退出
ll R = min(n - 1, i + 2 * r); //新建供电站的位置
diff[i] += m; //差分数组加左边界,即当前城市,前面遍历过去的可不管
if (R + 1 < n) diff[R + 1] -= m; //差分数组加右边界,此处判断是防止越界用
cur += m; //给当前城市加电
}
}
return true;
}
long long maxPower(vector<int> &stations, int r, int k) {
ll n = stations.size(), ans = -1;
//1.构造前缀和
vector<ll> sum(n + 1, 0), power(n, 0);
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + stations[i - 1];
}
//2.算power
for (int i = 0; i < n; i++) {
power[i] = sum[min((ll)n, (ll)i + r + 1)] - sum[max(0, i - r)];
}
ll left = stations[0], right = k;
for (auto x: stations) {
left = min(left, (ll)x);
right += x;
}
while (left <= right) {
ll mid = left + (right - left) / 2;
if (ok(power, r, (ll)k, mid, n)) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
};最后,我们来到了最cs的第四题:3464. 正方形上的点之间的最大距离 ,先看题。
题目拿到手我们可能会没啥思路,那就看看提示:
Think of the coordinates on a straight line in clockwise order.
翻译:把这些坐标按顺时针顺序,想象成排在一条直线上的点。
这就是我们这道题的主旋律。让我们跟着这个主旋律,慢慢的拆解这道题目,将其拿下。
首先,我们需要将这些坐标转换成排在一条直线上的点。有两条思路,第一条思路是模拟一个光标,以顺时针方向沿着正方形转一圈,然后采集点;第二条思路是直接去遍历点,然后判断点所在的边,直接转换成沿着正方形顺时针走的距离,最后将获得的一个个距离排序。这里我们选择第二条思路,因为模拟光标比较费时费力,虽然说也不难。我们使用如下转换方式:
if (x == 0) t = y; // 左边:从 (0,0) 向上
else if (y == side) t = side + x; // 上边:向右
else if (x == side) t = 3LL * side - y; // 右边:向下
else t = 4LL * side - x; // 下边:向左最后再排个序,我们的点与点直接的距离就生成完毕了。
好了,将这些点摊开分布在数轴上后,第二步就是想出判断mid行不行的算法了。再去理解一下题意:我们需要让任意两个点之间的最小曼哈顿距离最大化。那么啥时候两个点之间的曼哈顿距离最小呢?那就是两个挨在一起的点。换句话说,我们只需要考虑,我们选取的k个点按顺序排列后,两两之间的距离全都>=mid即可。
那么如何选点呢?这时候,我们的二分查找就要限时返厂了。我们可以开一个k次的循环,每次都用二分找最接近当前距离+mid的点,然后将当前距离更新成找到的新点,这样匍匐着往后移动。如果能找满k次,说明可以,否则不行。就像这样:
for (auto start: ps) {
ll end = start + side * 4LL - mid;
ll cur = start;
for (int i = 0; i < k - 1; i++) {
auto it = lower_bound(ps.begin(), ps.end(), cur + mid); //这里偷个懒,用stl库里面的lowerbound
if (it == ps.end() || *it > end) { //
cur = -1;
break;
}
cur = *it;
}
}那么问题来了,为啥我的外面还套着一层循环?上面二分找点看起来好像已经很完美了。
这其实是为了找最佳起点。因为从第一个起点开始不一定是最好的方案,我们得一个个试,只要从某一个点开始能跑通mid,就说明mid行;如果从所有点开始都跑不通mid,那说明mid是真不行。这就有点像01dp了,这个点可能选可能不选,最后放在最后一个点获得最佳结果。当然这道题也能用dp,但是不划算,以下是GPT5原文:
可以做成 DP—but 不划算。更具体地说:
结论先讲
- 若你还是采用“二分最小距离 D + 可行性判断”的框架,那么可行性判断既可以用贪心,也可以用一种0/1 风格的 DP。
- 但在这道题里,贪心更简单也更快;DP 做可行性判断通常会更慢、更麻烦,难以优于你现在的做法。
如果硬要用 DP,怎么设?
把点按周长坐标排序并扩一倍:
ext[i+n] = ext[i] + P,其中P = 4*side。
固定一个候选最小距离D(来自二分),预处理nxt[i] = 最小的 j >= i 且 ext[j] >= ext[i] + D然后在一个线性区间上做“选/不选”的 DP:
- 取某个起点 s(把圆在 s 处“切开”),允许的最远下标为
lim = upper_bound(ext, ext[s] + P - D) - 1
(保证最后选的点与起点的环向距离也 ≥ D)定义
f[i] = 在区间 [i..lim] 内能选择的最多点数 转移:f[i] = max( f[i+1], 1 + f[nxt[i]] ) // 选 or 不选 i 边界:f[lim+1] = 0- 若
f[s] >= k则 D 可行。这样看起来是标准的“01 选择跳转”DP。
复杂度问题
关键在于这是环,切口位置 s 不同,
lim不同,DP 的有效区间也不同。
如果你对每个 s 都跑一遍上述 DP,复杂度接近 (O(n^2))(尽管每次是 (O(\text{区间长度})))。在 (n) 可到 1.5 万的条件下,这会吃不消。贪心那边则是:
- 你现在的检查是:对每个起点 s,循环选择 (k-1) 次,每次
lower_bound一次。
复杂度大致 (O(n \cdot k \cdot \log n)),而 (k \le 25),所以非常可行。有没有“只做两次”的圆环 DP(像打家劫舍那样“选首/不选首”)?
遗憾的是不太行。打家劫舍模型只与相邻元素互斥;而这里互斥半径取决于距离 (D),一个点会与若干个后继冲突(直到距离达到 (D) 的第一个点)。所以简单的“两种情况(选首/不选首)各做一次线性 DP”不能覆盖所有冲突关系。
什么时候 DP 有价值?
- 如果题目 不要求固定选 k 个,而是“最多选多少”,DP 在一次判定里就能给出最大可选数;不过这题我们本来就只需判定“是否 ≥ k”,贪心同样能办到;
- 或者 (n) 很小(比如几百)时,用 DP 书写上更直观也无妨。
小结(给你可用的建议)
- 能做:二分 (D) → 用 “扩一倍 +
nxt+ 0/1 DP” 判定可行。- 不推荐:总体会比你现在的“二分 + 贪心(lower_bound 跳)”更慢、更复杂。
- 继续用现在的方案就好;若想更快,可把每次
lower_bound的起点限制在上一次命中位置之后,或改成“扩一倍 + 双指针前扫”,把每步的log n也省掉。
好了,回到正题。那么上面的end的取值式子是怎么来的呢?这是为了防止我选的点离起点过近,即和起点的距离小于mid,而且我检查不到,导致误判此mid正确。有了这个上界限制,它就取不到离起点过近的元素。
这样分析下来,基本思路已经讲完了。下面是完整代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
public:
bool ok(vector<ll> ps, int k, ll mid, int side) {
for (auto start: ps) {
ll end = start + side * 4LL - mid;
ll cur = start;
for (int i = 0; i < k - 1; i++) {
auto it = lower_bound(ps.begin(), ps.end(), cur + mid);
if (it == ps.end() || *it > end) { //如果取到了ps的外面,或者取到了离起点过近的点
cur = -1;
break;
}
cur = *it;
}
if (cur >= 0) return true;
}
return false;
}
int maxDistance(int side, vector<vector<int> > &points, int k) {
// 1. 直接映射到周长坐标 a ∈ [0, 4*side),再排序
vector<ll> arr;
arr.reserve(points.size());
for (auto &p: points) {
ll x = p[0], y = p[1], t = 0;
if (x == 0) t = y; // 左边:从 (0,0) 向上
else if (y == side) t = side + x; // 上边:向右
else if (x == side) t = 3LL * side - y; // 右边:向下
else t = 4LL * side - x; // 下边:向左
arr.push_back(t);
}
sort(arr.begin(), arr.end());
//2.开始二分
ll l = 0, r = side * 4LL / k, ans = -1;
while (l <= r) {
ll mid = l + (r - l) / 2;
if (ok(arr, k, mid, side)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
};4.6 第k小/大 1031更新
4.6.1 简介
站在10月的尾巴,我又来更新了。
先看看本次的做题情况:

后面的题目没做完,是因为我觉得除了前几道题,后面的题目对我进修二分并没法起到很大的作用。况且就业的刷题是主推hot100的,我现在还没开始刷,已经略有些晚了。接下来,我准备再解决贪心题单,然后直接转战hot100。所以下面的其他类型题目我就不做了。
老样子,给题目分个类:
1.基础题(我能较快做出来)
没有,实则从第一题开始就看题解了,还是比较有难度
2.进阶题(我需要思考一下才能做出来)
(讲解)668. 乘法表中第 K 小的数 这题属于是第k小/大类型二分题目的示例题目了
378. 有序矩阵中第 K 小的元素 这题同上,也是示例题目
(讲解)719. 找出第 K 小的数对距离 这题有点像滑动窗口的寻找最长合法子序列,和第k大第k小关系不大我觉得
3.困难题(大体思路正确,但是需要纠正一些细节后才能做对)
(讲解)878. 第 N 个神奇数字 1897 利用容斥原理算出有多少个a的倍数以及b的倍数比自己小,从而二分猜答案
1201. 丑数 III 2039 更高级的容斥原理,不讲,讲了也没啥用
786. 第 K 个最小的质数分数 2169 纯纯枚举法,n方复杂度也能解决,但是nlogn应该比较难
4.地狱题(我看了题解还得理解很久,才能彻底弄懂)
793. 阶乘函数后 K 个零 2100 纯纯公式题,我不好说,能推导出阶乘后面0的个数与5的因子的相关性的人能直接秒,其他人死活做不出
3116. 单面值组合的第 K 小金额 2387 纯纯78题啊,容斥原理+dfs枚举最小集合+二分,不讲,感兴趣的可以自己点力扣去看链接
5.78题(题解里面需要用到我目前没掌握的,且难以快速掌握的知识解决题目,所以看了题解也无法做出)
剩下没做的题目,默认78题
6.非二分查找题目
(讲解)373. 查找和最小的 K 对数字 用最小堆可以解决,作为题外话可以讲讲
1439. 有序矩阵中的第 k 个最小数组和 2134 同上,也是最小堆,不过条件比上面的苛刻
上面的题目,如果你想牢牢掌握这方面知识点,我个人认为,把668、378、878这三题搞懂就差不多了,其他题目能否做出纯纯看其他知识的造化。
4.6.2 开始讲解!
首先我们来看第一题:668. 乘法表中第 K 小的数,先看题。
首先,既然是二分猜答案,那我们的主要任务就是在猜一个答案后,判断一下这个答案到底是第几小/大。
这道题是乘法表,所以每一行的每个数都是第一个数的倍数。所以,我们只需要将这个数整除第一个数,就知道有几个数比它小了。然后我们再一行一行处理,就能得到每一行有几个数比当前这个数要小,最后再一累加就能得到这个数到底比乘法表里面多少个数大了。
好了,这样我们就知道了当前猜的答案是第几小的数了。然后,再配合二分算法,如果我是>k小的数,说明我猜大了,下一次猜小一点;反之,我下一次猜大一点。这样就能把答案猜出来了。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
public:
bool ok(int mid,int m,int n,int k) {
int cnt=0;
for (int i=1;i<=m;i++) {
cnt+=min(n,mid/i);
}
return cnt>=k;
}
int findKthNumber(int m, int n, int k) {
ll l=1,r=(ll)m*n+1,ans=-1;
while (l<=r) {
ll mid = l+(r-l)/2;
if (ok(mid,m,n,k)) { //如果cnt>=k-1,说明猜的数大了或者猜中了
ans = mid;
r = mid-1;
}else {
l = mid+1;
}
}
return ans;
}
};
接着我们来讲第二题:719. 找出第 K 小的数对距离,先看题。
这题的核心思路是和滑动窗口的满足条件的最短子串题型非常相似的。我引用一下我滑动窗口笔记里面的一段话:
初始化左边界left,计数器cnt。开一个循环遍历右边界right,使其一直往右推,直到不符合条件,然后进入子循环,将左边界left一直往右推,直到符合条件。此时,[left,right]这个区间已经是符合条件的了(这一点和2.3.1的方法不一样),由于是越短越合法,所以[left+1,right],[left+2,right]...[right,right]都是合法的子数组。所以我们直接在计数器cnt上累加上right-left+1,就是我们这次得到的子数组个数。然后主循环继续将右边界向右推,直到再次不符合条件,如此往复,直到到达边界。这样我们就能在一次次的左右边界的接力前进中得到所有符合条件的子数组个数,时间复杂度O(n)。
这道题也是非常类似,但是还是有一些区别,先看一下代码片段:
bool ok(int mid,vector<int>& nums,int k) {
int cnt=0;
for (int j=1;j<nums.size();j++) {
int i=0;
while (abs(nums[j]-nums[i])>mid && i<j) {
i++;
}
cnt+=j-i;
}
return cnt>=k;
}这里用了一个while条件循环,将i指针一直往后推,直到i和j之间的数的差距<=mid才停下。因为nums[j]-nums[i]符合条件,所以nums[j-1]-nums[i]....nums[i+1]-nums[i]肯定全都符合条件。是不是对味了?哈哈。
核心的代码逻辑解决后,其他地方就简单了,就是常规的二分。记得得先给nums升序排序。
class Solution {
public:
bool ok(int mid,vector<int>& nums,int k) {
int cnt=0;
for (int j=1;j<nums.size();j++) {
int i=0;
while (abs(nums[j]-nums[i])>mid && i<j) {
i++;
}
cnt+=j-i;
}
return cnt>=k;
}
int smallestDistancePair(vector<int>& nums, int k) {
//1.先给nums排序
sort(nums.begin(), nums.end());
//2.开始二分
int n = nums.size(),l=0,r=nums[n-1]-nums[0],ans=-1;
while (l<=r) {
int mid = l+(r-l)/2;
if (ok(mid,nums,k)) { //是答案或者偏大
ans = mid;
r = mid-1;
}else {
l = mid+1;
}
}
return ans;
}
};我们接着来看第三题:878. 第 N 个神奇数字,先看题。
我们知道要二分猜答案,所以我们现在的任务就是编写算法来算出我猜的这个数字在所有“神奇”数中是第几小的。
如果神奇数是a一个数的倍数,那我们天然的知道,这个数num是第num/a小的数。但是神奇数的定义是:
一个正整数如果能被a或b整除,那么它是神奇的。
它必须同时是a和b的倍数。这时候你直接num/a+num/b也不行,因为会有重复的部分。
那么我们如何去掉重复的部分呢?这时候就需要请出我们的容斥原理了。
先让ai讲解一下,啥是容斥原理:
🌟 一、基本思想
容斥原理(Principle of Inclusion-Exclusion)用于计算多个集合并集的元素个数。
它的思路是:先把每个集合的元素都算上,然后减去重复计算的部分,再加回多次被减的部分。🧩 二、两个集合的情况
对于两个集合 $A$ 和 $B$,有:
$$ |A \cup B| = |A| + |B| - |A \cap B| $$
解释:
- $|A| + |B|$ 把交集算了两次;
- 所以要减去一次 $|A \cap B|$。
🔢 三、三个集合的情况
对于三个集合 $A, B, C$,有:
$$ |A \cup B \cup C| = |A| + |B| + |C| * |A \cap B| - |A \cap C| - |B \cap C| - |A \cap B \cap C| $$
规律:
- 加上单个集合;
- 减去两两交集;
- 再加上三者交集。
💡 四、一般形式
对于 $n$ 个集合 $A_1, A_2, \dots, A_n$,有:
$$ \Big|\bigcup_{i=1}^{n} A_i\Big| = \sum_{i} |A_i| * \sum_{i<j} |A_i \cap A_j| - \sum_{i<j<k} |A_i \cap A_j \cap A_k| * \cdots - (-1)^{n+1} |A_1 \cap A_2 \cap \cdots \cap A_n| $$
🎯 五、应用举例
求 $1 \sim 100$ 中能被 2 或 3 整除 的数的个数。
设
- $A$:能被 2 整除的数,$|A| = 50$
- $B$:能被 3 整除的数,$|B| = 33$
- $A \cap B$:能被 6 整除的数,$|A \cap B| = 16$
根据容斥原理:
$$ |A \cup B| = 50 + 33 - 16 = 67 $$
因此共有 67 个数 能被 2 或 3 整除
这道题所涉及到的容斥原理,是上面讲解的两个集合的情况,所以我们只需要减去一次$|A \cap B|$即可。
那么我们该如何计算这个$|A \cap B|$呢?这时候就需要用到最小公倍数的知识了。
举个例子,在同时是3和4倍数的所有数里面,比20小的有几个呢?可得3和4的最小公倍数为12,所以只有1个,也就是20/12=1。
好了,到这里,这道题目就做完了。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MOD = 1000000000+7;
class Solution {
public:
bool ok(ll mid,int n,int a,int b) {
ll cnt = mid/a+mid/b-mid/lcm(a,b); //利用两个数的容斥原理计算比mid小的数的个数
return cnt>=n;
}
int nthMagicalNumber(int n, int a, int b) {
ll l = min(a,b)+n-1,r = 1LL*min(a,b)*n,ans=-1;
while (l<=r) {
ll mid = l+(r-l)/2;
if (ok(mid,n,a,b)) { //猜大了或者就等于答案
ans = mid%MOD;
r = mid-1;
}else {
l = mid+1;
}
}
return ans;
}
};最后,我们来讲第四题:373. 查找和最小的 K 对数字 ,这就不是二分的知识点了。
这道题虽然也可以用二分做,但是我看了做法感觉过于牵强,所以还是转战最小堆了。
那么啥是最小堆呢?不管它的内部原理,它的作用就是:你加数进去,自动把最小的放在堆顶(top)供你取用。即使你弹数出去,它也一直保持最小的数在堆顶。
但是要澄清一点,c++的priority_queue(优先队列)默认是最大堆,也就是默认堆顶是最大的数。所以我们要么在后面加参数,要么就简单粗暴,直接把我们要对比的key设为负数,直接搞定。
好了,知道了最小堆这个概念,对做这个题目又有什么用呢?
题目要求找前k个和最小的数对,你的第一反应肯定是用双层循环一一配对两层数组中的每个数,但是这样太慢了,时间不允许。
首先,我们知道,(0,0)一定是第一小的数对,因为两个数组是升序排的。那么第二小的会是谁呢?无法确定,可能是(1,0)也可能是(0,1),因为两个数组从第一个数到第二个数的增长幅度不一定一样。然后假设是(1,0)第二小吧,那(0,1)就是第三小,那么第四小呢?可能是(2,0),(1,1),(0,2),这样就有三种可能了。这样还是过于麻烦了,即使配合最小堆使用,也不太方便。
那么我们是否可以开局直接将(0,0),(1,0),(2,0)...(i,0)全部入堆呢?这样,我们就只需要管第二个数组了,因为第一个数组已经被我们枚举完了。用刚刚同样的方法来分类讨论:(x,y)如果是第k小,那么第k+1小就有可能是(x+1,y)或者(x,y+1)。由于我们已经把(i,0)全入堆了,所以x就不需要动了,因为我们每个x都有,只需要用(x,y+1)往后推y就已经能包含(x+1,y)的情况了!所以,我们此时只需要入堆(x,y+1)即可,记得判断一下是否越界。
按照上面的过程,我们一直取堆顶,直到取够k个,就能找到第k小的数对了。
看代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
//1.先将(i,0)全部入堆
priority_queue<tuple<int,int,int>> q;
for (int i=0;i<nums1.size();i++) {
q.emplace(-nums1[i]-nums2[0],i,0); //堆顶记得用负数
}
//2.再开始取满k个值
vector<vector<int>> ans;
for (int i=0;i<k;i++) {
auto [_,x,y] = q.top();
q.pop();
ans.emplace_back(vector<int>{nums1[x],nums2[y]});
if (y+1<nums2.size()) {
q.emplace(-nums1[x]-nums2[y+1],x,y+1);
}
}
return ans;
}
};结语
二分查找的部分就讲解到这里了,接下来我将进军dp题单。如果觉得我讲的不错,欢迎继续关注我的博客!
